Question

Решите, пожалуйста, приложенные задачи. Минимальные пояснения должны быть ​

Answer 1

Ответ:

1) Расстояние от центра сферы до линии пересечения плоскостей равно 2√6 ед.

2) Радиус шара равен $\displaystyle \frac{3\sqrt{3} }{\sqrt[3]{2} }$ ед.

Объяснение:

1) Найти расстояние от центра сферы до линии пересечения плоскостей.

2) Найти радиус шара, описанной около правильной пирамиды.

1)

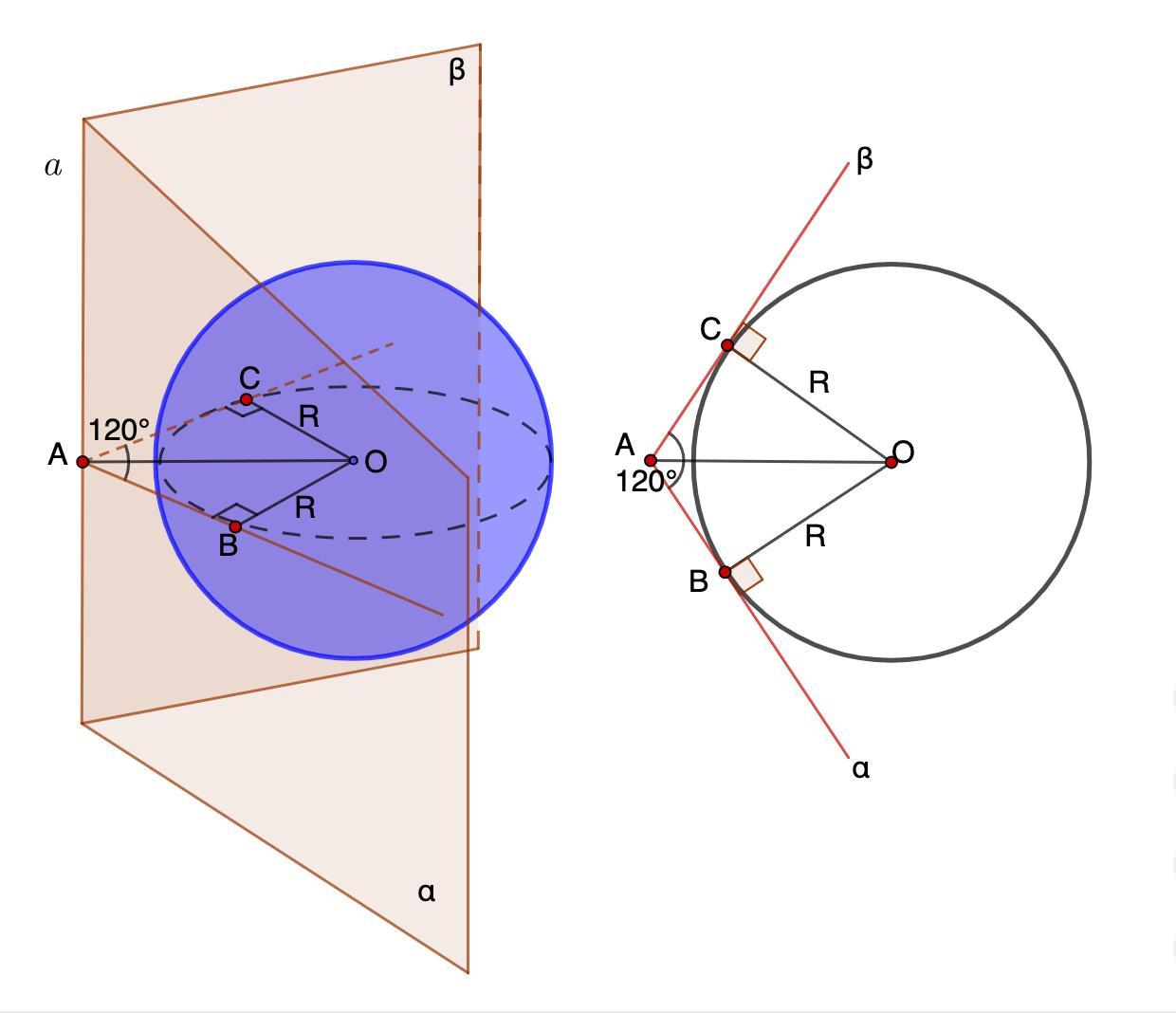
Дано: Сфера О;

α и β касаются сферы в точках В и С;

α ∩ β = a; A ∈ a;

Угол между α и β = 120°;

S сферы = 72π

Найти: АО.

Решение:

Построим сечение через центр сферы О, перпендикулярное линии пересечения α и β - прямой а.

∠CAВ = 120° - линейный угол двугранного угла между α и β.

1. Найдем радиус сферы.

• Площадь сферы находится по формуле:
• S сферы = 4πR²

72π = 4πR²

R² = 18

R = 3√2

2. Рассмотрим ΔАСО.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ΔАСО - прямоугольный.

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ ∠ОАС = ∠ВАС : 2 = 60°

• Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle sin\angle{OAC}=\frac{R}{AO}\\ \\AO = \frac{R}{sin\;60^0}=\frac{3\sqrt{2} \cdot2}{\sqrt{3} } =\frac{3\sqrt{2}\cdot2\cdot\sqrt{3} }{\sqrt{3}\cdot\sqrt{3} } =2\sqrt{6}$

Расстояние от центра сферы до линии пересечения плоскостей равно 2√6 ед.

2)

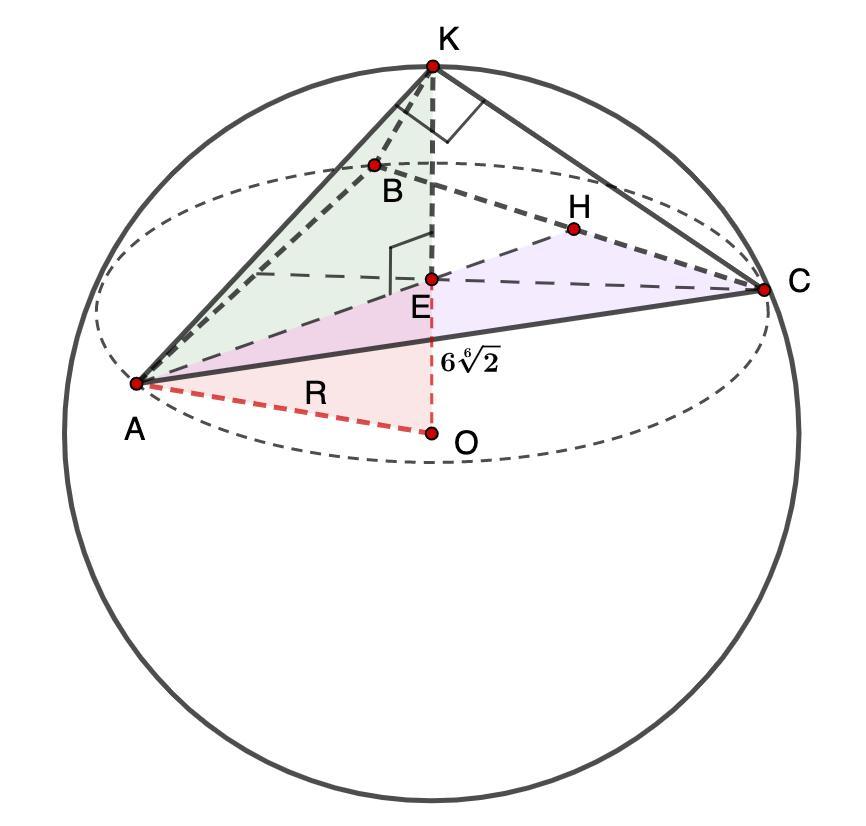
Дано: КАВС - правильная пирамида.

Сфера О - описана около КАВС;

АК ⊥ КС; КС ⊥ КВ; КВ ⊥ АК;

АС = $6\sqrt[6]{2}$.

Найти: R шара.

Решение:

• В правильной пирамиде в основании лежит правильный треугольник, а боковые грани - равнобедренные треугольники.

1. Рассмотрим ΔАВС - равносторонний.

• В равностороннем треугольнике высоты, медианы и биссектрисы совпадают и пересекаются в одной точке.

АН - высота, медиана.

⇒ ВН = НС = $6\sqrt[6]{2} : 2 = 3\sqrt[6]{2}$;

2. Рассмотрим ΔАНС - прямоугольный.

• В равностороннем градусная мера углов равна 60°.

$\displaystyle sin \angle{ACH}=\frac{AH}{AC}=\\\\AH= sin\;60^0\cdot{AC}=\frac{\sqrt{3} }{2}\cdot6\sqrt[6]{2}=3\sqrt{3}\sqrt[6]{2}$

3. Рассмотрим ΔАКС - прямоугольный, равнобедренный.

По теореме Пифагора:

АК² + КС² = АС²

или

2АК² = 36∛2

АК² = 18∛2

4. Рассмотрим ΔАКЕ - прямоугольный.

• Медианы треугольника точкой пересечения делятся в отношении 2 : 1, считая от вершины.

⇒ $AE=2\sqrt{3}\sqrt[6]{2}$

По теореме Пифагора найдем КЕ:

КЕ² = АК² - АЕ² = 18∛2 - 12∛2 = 6∛2

$KE=\sqrt{6}\sqrt[6]{2}$

5. Рассмотрим ΔАЕО - прямоугольный.

АО = R;

EO = R - EK = R - $\sqrt{6}\sqrt[6]{2}$

По теореме Пифагора:

$\displaystyle R^2=AE^2+EO^2 = 12\sqrt[3]{2}+(R-\sqrt{6}\sqrt[6]{2})^2\\ \\ R^2=12\sqrt[3]{2}+R^2-2R\sqrt{6} \sqrt[6]{2}+6\sqrt[3]{2}\\ \\ 2R\sqrt{6}\sqrt[6]{2} =18\sqrt[3]{2}\\ \\ R=\frac{18\sqrt[3]{2} }{2\sqrt{6} \sqrt[6]{2} } \\\\R=\frac{9\sqrt[6]{2} \sqrt{6} }{6}\\ \\R=\frac{3\sqrt[6]{2}\sqrt{3}\sqrt[6]{2^3} }{2} \\\\R=\frac{3\sqrt{3} }{\sqrt[3]{2} }$

Радиус шара равен $\displaystyle \frac{3\sqrt{3} }{\sqrt[3]{2} }$ ед.