Прямая y=-4x+1 является касательной к графику функции y=x²-5x+7. Найдите абсциссу точки касания
Помогите с решением пж
Ответы
Ответ:
Прямая y₁ = -4x + 1 не является касательной к графику функции
y₂ = x² - 5x + 7 и не имеет с ним общих точек.
Объяснение:
Найти абсциссу точки касания прямой y₁ = -4x + 1 с графиком функции y₂ = x² - 5x +7.
- Касательной к графику функции y=f(x) в точке (x₀;f(x₀)) называют прямую, проходящую через точку (x₀;f(x₀)), с отрезком которой практически сливается график функции при значениях х сколь угодно близких к x₀.
I. Касательная имеет одну общую точку с графиком функции.
Тогда точка касания принадлежит графикам каждой функции.
В точке касания y₁ = y₂.
Решим уравнение:
x² - 5x +7 = -4x + 1;
x² - x + 6 = 0;
D = b² - 4ac = 1² - 4·6 = 1 - 24 = -23;
D < 0.
Уравнение не имеет решений.
Прямая y₁ = -4x + 1 не является касательной к графику функции
y₂ = x² - 5x +7.
II. Подойдем к вопросу с другой стороны.
1) Угловой коэффициент касательной k равен значению производной функции в точке касания.
y₁ = -4x + 1;
k = -4;
y₂'(x₀) = -4.
2) Найдем производную функции y₂ = x² - 5x +7.
y₂' = (x² - 5x +7)' = 2x - 5;
Определим абсциссу x₀ точки, в которой касательная с угловым коэффициентом k = -4 касается графика функции.
2x - 5 = -4;
2x = 1;
x = 0,5.
Касательная с угловым коэффициентом k = -4 касается графика функции y₂ = x² - 5x +7 в точке с абсциссой x₀ = 0,5.
3) Найдем уравнение этой касательной.
- Уравнение касательной определяется по формуле:
y = f'(x₀)(x - x₀)+f(x₀).
f'(x₀) = k = -4;
(x - x₀) = x - 0,5;
f(x₀) = 0,5² - 5·0,5 + 7 = 0,25 - 2,5 + 7 = 4,75.
y = -4·(x - 0,5) + 4,75 = -4x + 2 + 4,75 = -4x + 6,75.
Уравнение касательной, проходящей через точку x₀ = 0,5 имеет вид:
y = -4x + 6,75.
Как видим линейные функции
y = -4x + 6,75 и y₁ = -4x + 1
не совпадают.
Их графики параллельны, так как угловые коэффициенты равны.
Прямая y₁ = -4x + 1 не является касательной к графику функции
y₂ = x² - 5x + 7 и не имеет с ним общих точек.
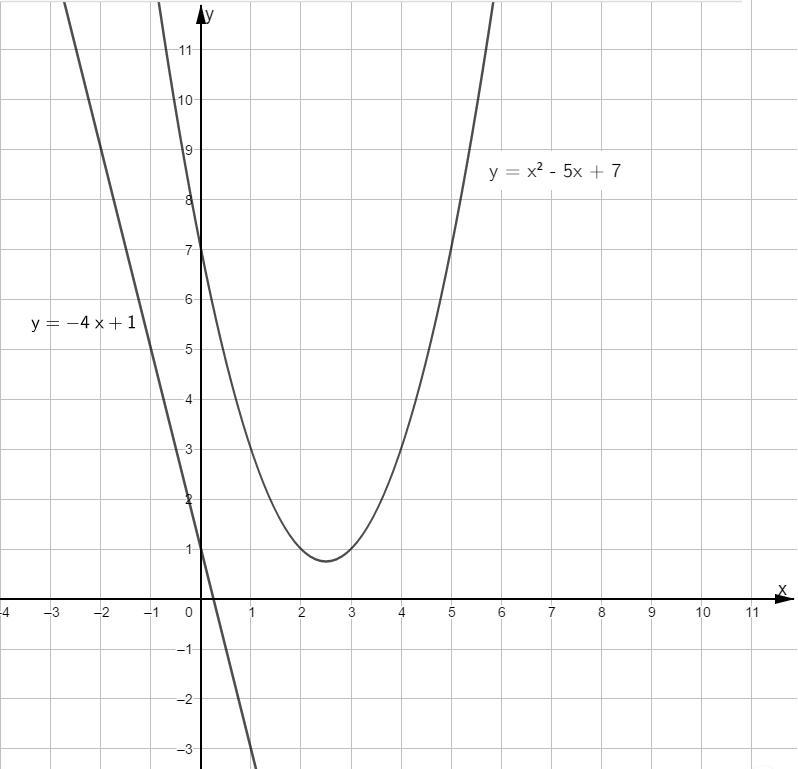
Это подтверждается при построении графиков функций (в приложении).
#SPJ1
проверьте условие