Предмет: Алгебра,
автор: dfgddffxx
помогите пожалуйста решить
Приложения:
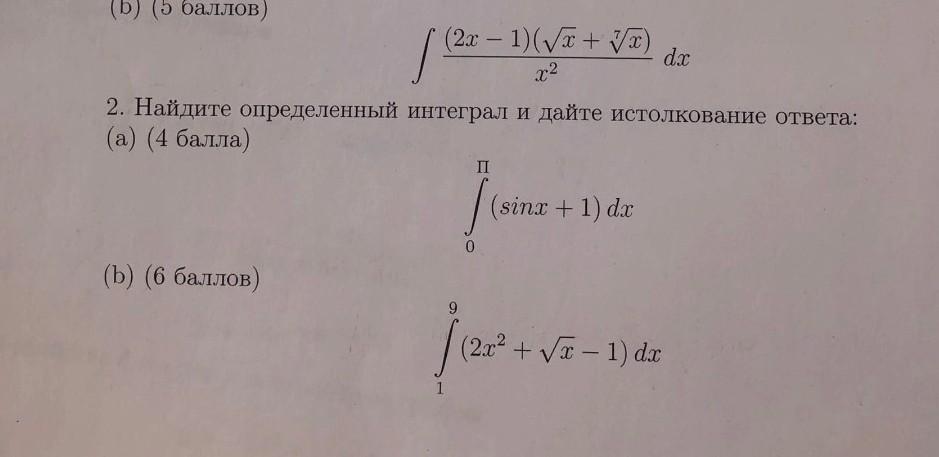
Ответы
Автор ответа:
2
Ответ:
olgaua64:
В в) ошибка
Автор ответа:
1
Відповідь:
Пояснення:
Приложения:

спасибо большое
:)
Похожие вопросы
Предмет: Немецкий язык,
автор: Елисей141
Предмет: Русский язык,
автор: YTKotansky
Предмет: Қазақ тiлi,
автор: ydxjckcyd273378
Предмет: Английский язык,
автор: irina25526
Предмет: Қазақ тiлi,
автор: rashidam1991gmailcom