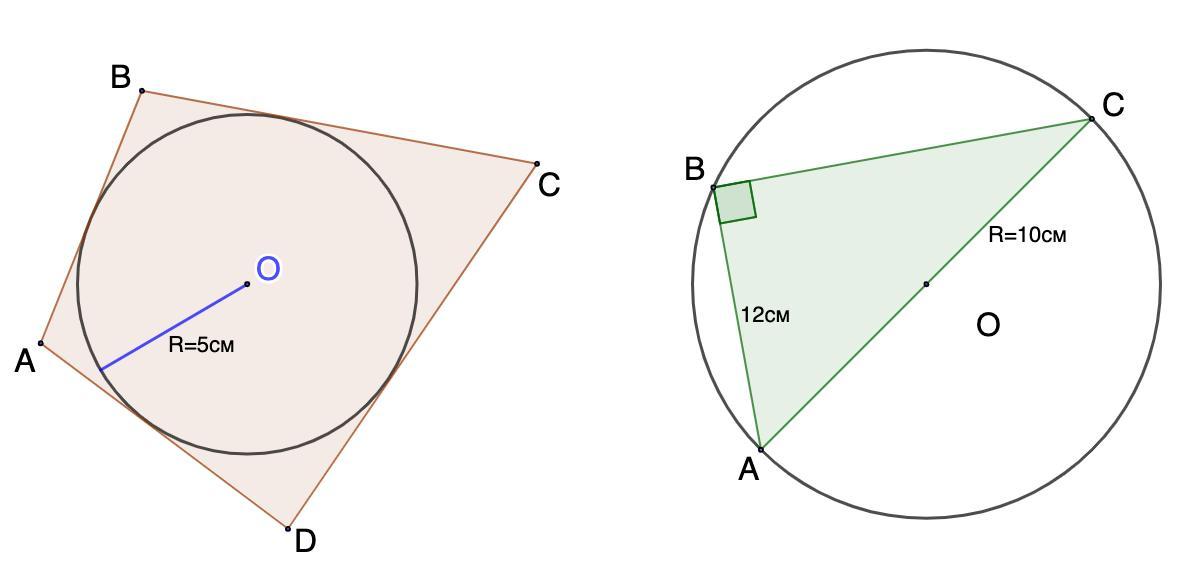
2.Сумма двух противоположных сторон описанного четырёхугольника равна 16см.Радиус равен 5см. Найти площадь четырёхугольника.
3.Около прямоугольного треугольника описана окружность радиуса 10см.Найти периметр и площадь треугольника, если один из катетов равен 12см.
Ответы
Ответ:
2. Площадь четырёхугольника равна 80 см².
3. Периметр треугольника равен 48 см, площадь равна 96 см.
Объяснение:
2. Сумма двух противоположных сторон описанного четырёхугольника равна 16 см. Радиус равен 5 см. Найти площадь четырёхугольника.
3. Около прямоугольного треугольника описана окружность радиуса 10 см. Найти периметр и площадь треугольника, если один из катетов равен 12 см.
2.
Дано: ABCD - четырехугольник;
Окр.О,R - вписанная;
AB + CD = 16 см;
R = 5 см.
Найти: S (ABCD).
Решение:
- Если в четырехугольник вписана окружность, то суммы противоположных сторон равны.
⇒ AB + CD = BC + AD = 16 см.
- Периметр - сумма длин всех сторон четырехугольника.
⇒ Р = AB + CD + BC + AD = 16 + 16 = 32 (см)
- Площадь четырехугольника, в который вписана окружность равна:
- S = pR, где р - полупериметр, R - радиус вписанной окружности.
р = Р : 2 = 32 : 2 = 16 (см)
R = 5 см
⇒ S (ABCD) = 16 · 5 = 80 (см²)
Площадь четырёхугольника равна 80 см².
3.
Дано: ΔАВС - прямоугольный;
Окр.О,R - описана около ΔАВС;
R = 10 см; АВ = 12 см.
Найти: Р (АВС); S (АВС).
Решение:
- Прямой вписанный угол опирается на диаметр окружности.
⇒ АС - диаметр.
АС = 2R = 20 см.
По теореме Пифагора найдем ВС:
ВС² = АС² - АВ²
ВС² = 400 - 144 = 256
ВС = √256 = 16 (см)
- Периметр треугольника - сумма длин всех сторон.
Р (АВС) = АВ + ВС + АС = 12 + 16 + 20 = 48 (см)
- Площадь прямоугольного треугольника равна половине произведения катетов.
Периметр треугольника равен 48 см, площадь равна 96 см.
#SPJ1