Предмет: Алгебра,
автор: zemlyanichka50
найти производное функции y = (2x^4– cosx)^11
Ответы
Автор ответа:
0
Ответ:
......................................
Приложения:
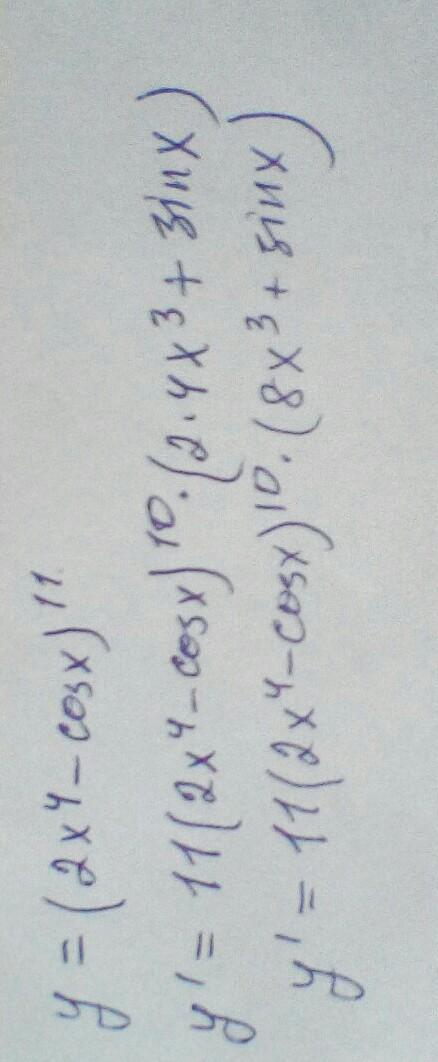
Автор ответа:
0
Ответ:
10*(2x^4– cosx)^10*8*x^3+sin(x)
Объяснение:
Для этого случая воспользуемся формулой производной для сложной функции: f(g(x))' = f'(g(x) * g'(x). То есть одна функция как бы "обёрнута" в другую. В нашем случае 2x^4– cos(x) "обёрнута" в степенную функцию.
Воспользуемся нашей формулой и получим первую часть выражения: ((2x^4– cosx)^11)' = 11*(2x^4– cosx)^10.
Теперь найдём производную "внутреней" части, то есть (2x^4– cosx). Производная разности равна разности производных, так что (2x^4– cosx)' = 8*x^3+sin(x).
Итоговый ответ, таким образом: 11*(2x^4– cosx)^10*(8*x^3+sin(x)).
Похожие вопросы
Предмет: Русский язык,
автор: ivanovmihail200
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Українська мова,
автор: mariannagetsko
Предмет: Химия,
автор: Nafanya15
Предмет: Алгебра,
автор: shubinPro