Предмет: Математика,
автор: miller2212
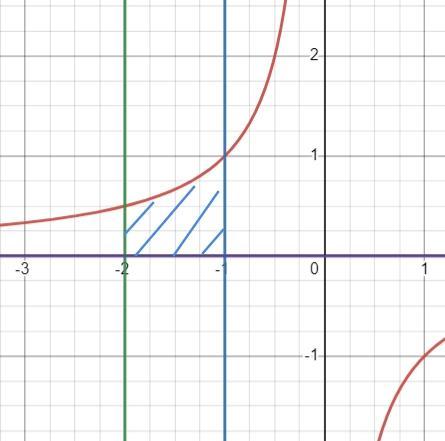
Найти площадь фигуры, образованную линиями:
y=-1/x, y=0, x=-1, x=-2
Ответы
Автор ответа:
1
Ответ:
S = ln(2)
Пошаговое объяснение:
Рисуем график, определяемся с фигурой, с пределами интегрирования и ищем площадь по формуле Ньютона-Лейбница
В нашем случае
b = -2
a = -1
y₁(x) = -1/x
y₂(x) = 0
Считаем интеграл
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: кравченкоюлия
Предмет: Английский язык,
автор: лиза2085
Предмет: Русский язык,
автор: мома01062005
Предмет: Алгебра,
автор: elisavetagrant
Предмет: Математика,
автор: ingastoryp0hng1