Question

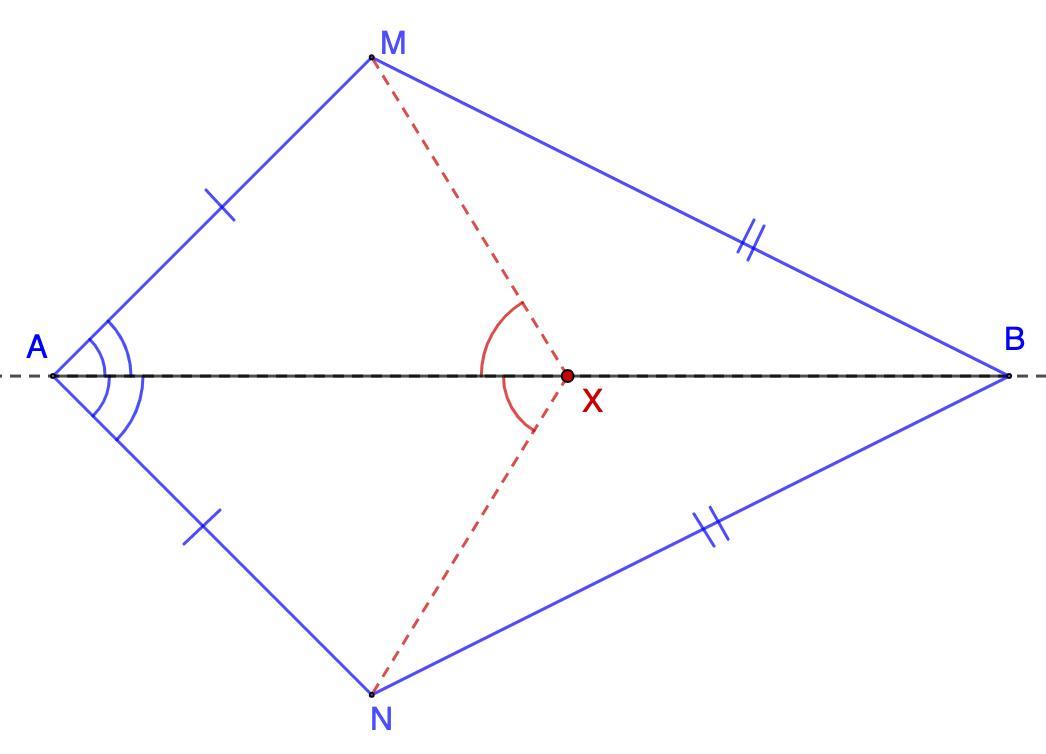
Точки M i N розміщені по рiзнi боки від прямоï АВ так, що MA = NA , MB = NB X довiльна точка відрізка АВ. Дове діть, що angle AXM= angle AXN


срочно!!!​

Answer 1

Ответ:

Доказано, что ∠AXM = ∠AXN.

Объяснение:

Точки M и N размещены по разные стороны от прямой АВ так, что MA = NA, MB = NB.  X - произвольная точка отрезка АВ. Доказать, что ∠AXM= ∠AXN.

Дано: АВ - прямая.

MA = NA, MB = NB;

Х ∈ АВ;

Доказать: ∠AXM= ∠AXN.

Доказательство:

1. Рассмотрим ΔАМВ и ΔАВN.

MA = NA, MB = NB (условие)

АВ - общая.

⇒ ΔАМВ = ΔАВN (по трем сторонам, 3 признак)

• В равных треугольниках против равных сторон лежат и равные углы.

⇒ ∠MAB = ∠NAB.

2. Рассмотрим ΔАМХ и ΔANX.

AM = AN (условие)

АХ - общая;

∠MAB = ∠NAB (п.1)

⇒ ΔАМХ = ΔANX (по двум сторонам и углу между ними, 1 признак)

⇒ ∠AXM = ∠AXN (как соответственные элементы)

Доказано, что ∠AXM = ∠AXN.

#SPJ1