Предмет: Геометрия,
автор: reksikbohatirov
знайдіть менший катет прямокутного трикутника якщо його гіпотенуза більша за один з катетів на 2 см, а за другий на 9. ЧАСУ МАЛО!!! 30 БАЛІВ ВСЕ ЩО Є
Приложения:

Ответы
Автор ответа:
2
Ответ:
Меньший катет прямоугольного треугольника равен 8 см
Объяснение:
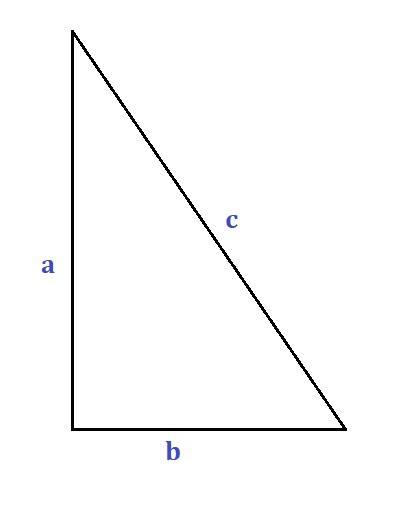
Пусть гипотенуза с прямоугольного треугольника равна х см, тогда, согласно условию, катет а = с - 2 = (х-2) см, а катет b = c - 9 = (x-9) cм.
( Если гипотенуза больше катета на 2 см, значит катет меньше гипотенузы на 2 см. Со вторым катетом - аналогично)
По теореме Пифагора: квадрат гипотенузы равен сумме квадратов его катетов, имеем:
с²=а²+b²
x²=(x-2)²+(x-9)²
x²-4x+4+x²-18x+81=x²
x²-22x+85=0
По теореме Виета найдём корни квадратного уравнения:
x₁=17, x₂=5
Найдём катеты прямоугольного треугольника:
- При x₁=17:
а = х-2= 17-2 = 15 см
b = x-9 = 17 - 9 = 8 см
- При x₂=5:
а = х-2= 5-2 = 3 см
b = x-9 = 5 - 9 = -4 см ⇒ x₂=5 - сторонний корень, т.к. катет не может быть меньше нуля.
Таким образом, меньший катет прямоугольного треугольника равен 8 см
#SPJ1
Приложения:
reksikbohatirov:
Я в шоке, вы для меня герой. Очень классное объяснение, спасибо вам
Спасибо, приятно
Похожие вопросы
Предмет: Другие предметы,
автор: Loyra
Предмет: Қазақ тiлi,
автор: ДанилВас1
Предмет: Русский язык,
автор: плей2
Предмет: Музыка,
автор: Яська2017
Предмет: Қазақ тiлi,
автор: regi23