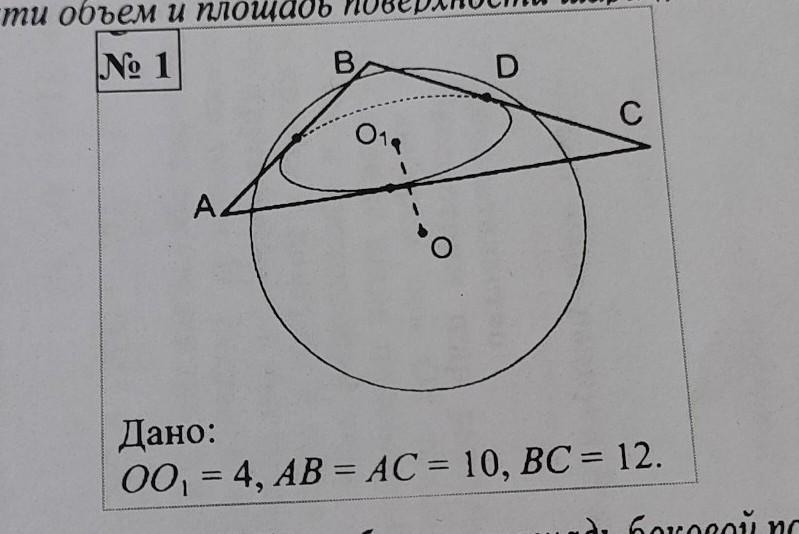
О-центр шара ,О1 и О2-центры кругов-сечений шара плоскостью.Найти объем и площадь поверхности шара.
Ответы
Ответ:
Объема шара равен (500π/3) кубических единиц, а площадь его поверхности равна 100π квадратных единиц
Примечание:
S₁ - площадь поверхности шара
Объяснение:
Дано: O - центр шара, O₁ - центр окружности вписанной в ΔABC,
OO₁ = 4, AB = AC = 10, BC = 12
Найти: V,S₁ - ?
Решение:
Пусть r - радиус окружности вписанной в треугольник ΔABC,
p - полупериметр треугольника ΔABC.
Пусть R - радиус шара.
По определению полупериметра:
p = (AB + BC + AC) / 2 = (10 + 12 + 10) / 2 = 32 / 2 = 16.
По формуле площади Герона (ΔABC):
S = √(p (p - AB)(p - BC)(p - AC)) = √(16 (16 - 10)(16 - 12)(16 - 10)) =
= √(16 * 6 * 4 * 6) = √(2304) = 48 квадратных единиц.
По формуле площади (ΔABC):
S = pr ⇒ r = S / p = 48 / 16 = 3
Рассмотрим прямоугольный треугольник ΔOO₁D (OO₁ ⊥ OD по теореме). По определению отрезок O₁D - радиус вписанной окружности, тогда O₁D = r = 3.
По теореме Пифагора:
OD = √(OO₁² + O₁D²) = √(4² + 3²) = √(9 + 16) = √25 = 5.
По определению OD - радиус шара, то есть R = OD = 5.
По формуле объема шара:
V = (4/3) * πR³ = (4/3) * 125π = (500π/3) кубических единиц
По формуле площади поверхности шара:
S₁ = 4πR² = 4π * 25 = 100π квадратных единиц
#SPJ1