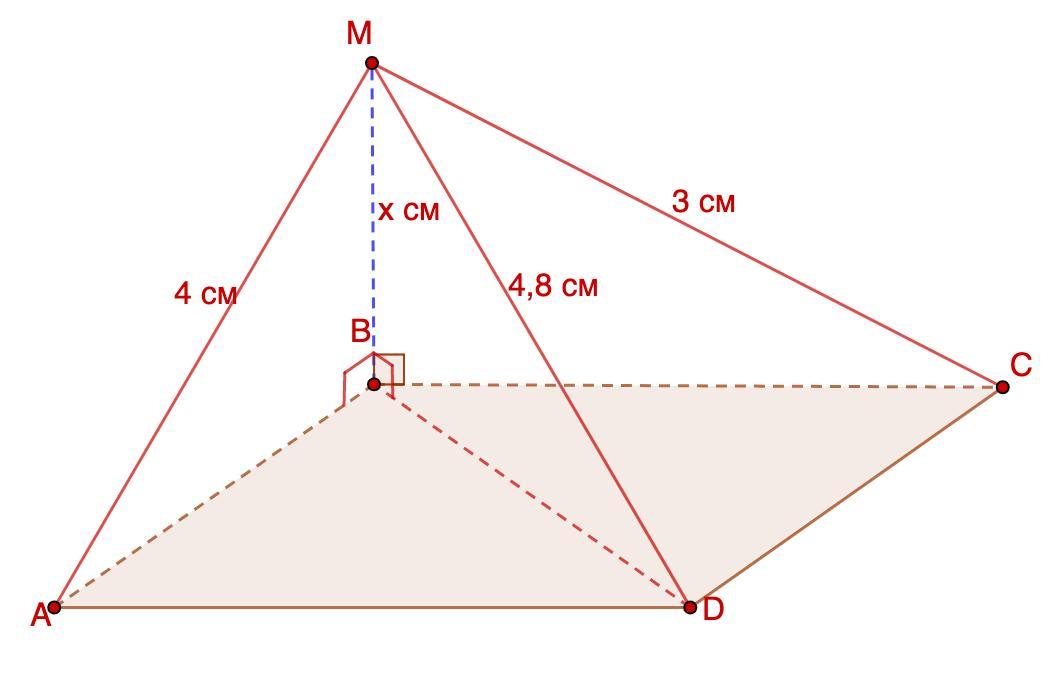
Через вершину B прямокутника ABCD проведено пряму BM, перпендикулярну до його площини. MA=4 см; MD=4,8 см; MC=3 см. Знайдіть:
1) MB
2) Площу прямокутника ABCD
Ответы
Ответ:
1) MB = 1,4 см.
2) Площадь прямоугольника ABCD равна 9,94 см².
Объяснение:
Через вершину B прямоугольника ABCD проведена прямая BM, перпендикулярная к его площади. MA = 4 см; MD = 4,8 см; MC = 3 см. Найти:
1) MB;
2) Площадь прямоугольника ABCD.
Дано: ABCD - прямоугольник;
ВМ ⊥ ABCD;
MA = 4 см; MD = 4,8 см; MC = 3 см.
Найти: 1) ВМ; 2) S (ABCD).
Решение:
1)
- Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в данной плоскости.
⇒ ВМ ⊥ АВ; ВМ ⊥ ВС; ВМ ⊥BD.
Пусть ВМ = х см.
1. Рассмотрим ΔВМС - прямоугольный;
По теореме Пифагора:
ВС² = МС² - ВМ² = 9 - х² (1)
2. Рассмотрим ΔАМВ - прямоугольный;
По теореме Пифагора:
АВ² = АМ² - ВМ² = 16 - х² (2)
3. Рассмотрим ΔABD - прямоугольный;
- Противоположные стороны прямоугольника равны.
⇒ ВС = AD
По теореме Пифагора:
ВD² = AB² + AD²
Подставим значение AB² и AD² из равенств (1) и (2)
ВD² = 16 - х² + 9 - х² = 25 - 2х²
4. Рассмотрим ΔВМD - прямоугольный.
По теореме Пифагора:
ВМ² = MD² - BD²
x² = 23,04 - 25 + 2х²
x² = 1,96
x = 1,4
MB = 1,4 см.
2)
Найдем площадь ABCD.
- Площадь прямоугольника равна произведению смежных сторон.
ВС² = 9 - х² = 9 - 1,96 = 7,04
ВС = √7,04 (см)
АВ² = 16 - х² = 16 - 1,96 = 14,04
АВ = √14,04 (см)
S (ABCD) = BC · AD = √7,04 ·√14,04 ≈ 9,94 (см²)
#SPJ1