6 класс найдите решение систем уравнений
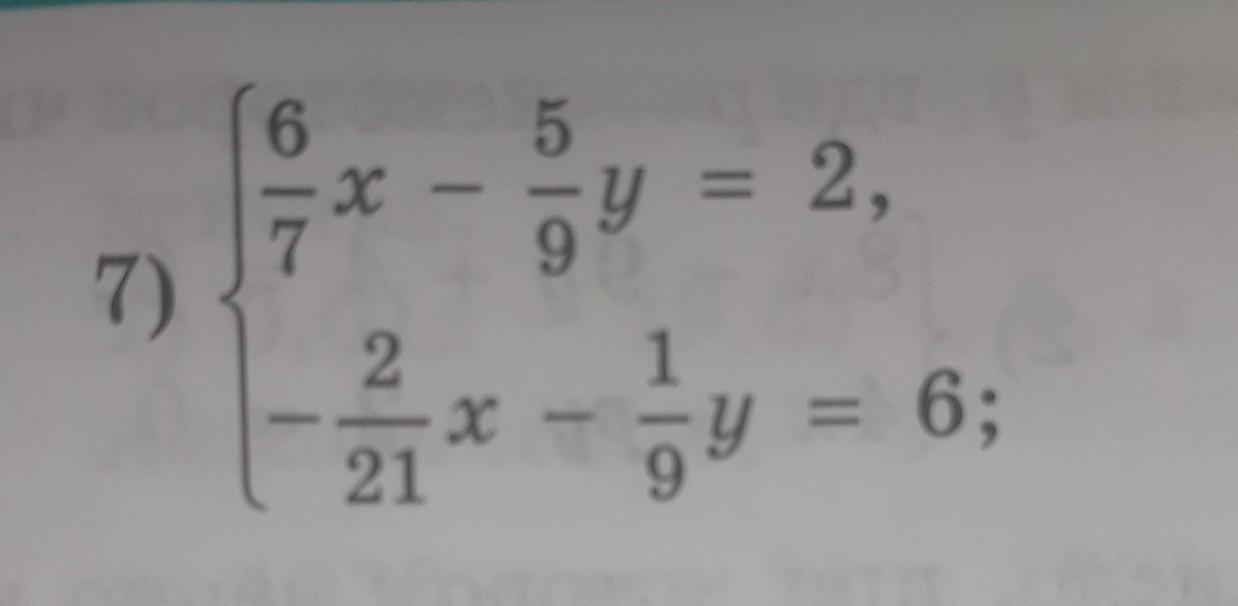
Ответы
Ответ:
В решении.
Пошаговое объяснение:
6х/7 - 5у/9 = 2
-2х/21 - у/9 = 6
Умножить все части первого и второго уравнения на 63, чтобы избавиться от дробного выражения:
9 * 6х - 7 * 5у = 63 * 2
3 * (-2х) - 7 * у = 63 * 6
↓
54х - 35у = 126
-6х - 7у = 378
Умножить второе уравнение на 9, чтобы решить систему сложением:
54х - 35у = 126
-54х - 63у = 3402
Сложить уравнения:
54х - 54х - 35у - 63у = 126 + 3402
-98у = 3528
у = 3528 : (-98)
у = -36;
Теперь подставить значение у в любое из двух уравнений системы и вычислить х:
54х - 35у = 126
54х = 126 + 35 * (-36)
54х = 126 - 1260
54х = -1134
х = -1134 : 54
х = -21;
Решение системы уравнений: (-21; -36).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
Пошаговое объяснение:
6/7х - 5/9у = 2 | * 63
-2/21х - 1/9у = 6 | * 63
54х - 35у = 126 | : -5
-6х - 7у = 378
-10,8х + 7у = -25,2
-6х - 7у = 378
-16,8х = 352,8
-6х - 7у = 378
1)
-16,8х = 352,8
х = 352,8 : (-16,8)
х = -21
2)
-6х - 7у = 378
-6*(-21) - 7у = 378
126 - 7у = 378
7у = 126 - 378
7у = -252
у = -252 : 7
у = -36
Ответ: (-21; -36)