Question

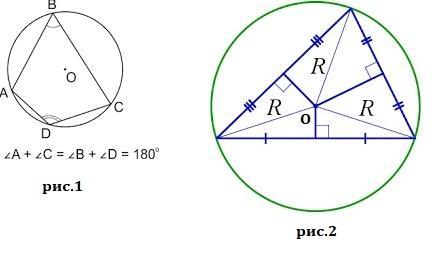
Выбери верное утверждение.

Если сумма противоположных углов четырёхугольника равна 180 ° , то около него можно описать окружность

Около треугольника можно описать бесконечно много окружностей

Около любого четырёхугольника можно описать окружность

Answer 1

Ответ:

Верные утверждения :

1)Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность

Объяснение:

Рассмотрим утверждения:

1) Если сумма противоположных углов четырёхугольника равна 180 ° , то около него можно описать окружность - ВЕРНО

Существует теорема: Если в четырёхугольнике сумма двух противоположных углов равна 180°, то около такого четырёхугольника можно описать окружность. (рис.1)

2) Около треугольника можно описать бесконечно много окружностей - НЕВЕРНО

Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника. Так как у каждого треугольника точка пересечения серединных перпендикуляров только одна, следовательно вокруг него можно описать только одну окружность. (рис.2)

3) Около любого четырёхугольника можно описать окружность - НЕВЕРНО

Можно описать окружность только вокруг четырёхугольника у которого сумма противоположных углов равна 180°.

(Например, у ромба сумма противоположных углов не равна 180°, вокруг него нельзя описать окружность.

Если бы мы нашли ромб, у которого сумма противоположных углов была бы равна 180°, то т.к. противоположные углы ромба равны, то каждый из этих углов был бы равен 180°:2=90°, а ромб с прямыми углами - это уже квадрат)

#SPJ1