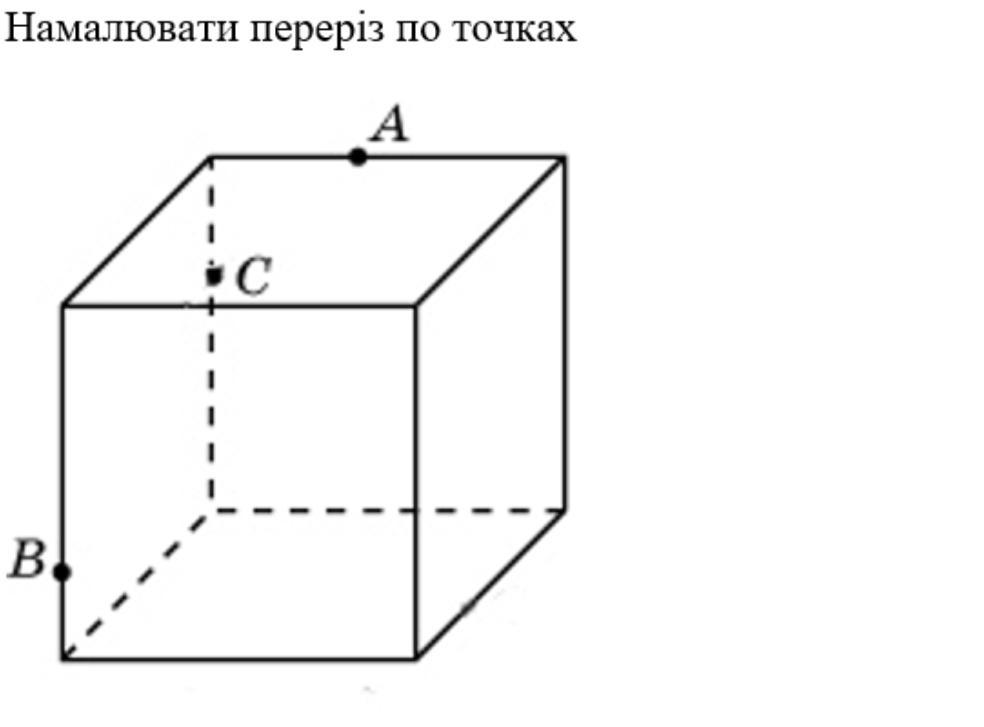
переріз куба через три точки
Ответы
Ответ:
Объяснение:
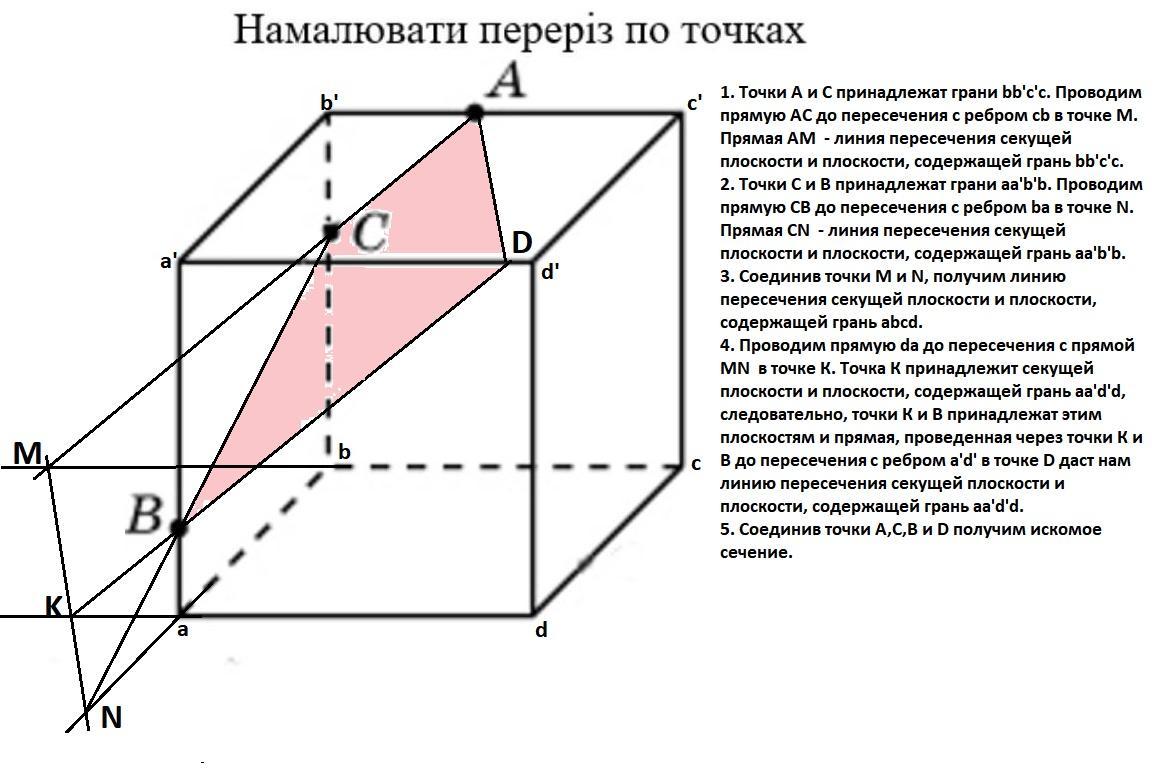
1. Точки А и С принадлежат грани bb'c'c. Проводим прямую АС до пересечения с ребром сb в точке М.
Прямая АМ - линия пересечения секущей плоскости и плоскости, содержащей грань bb'c'c.
2. Точки С и В принадлежат грани aa'b'b. Проводим прямую CB до пересечения с ребром ba в точке N.
Прямая CN - линия пересечения секущей плоскости и плоскости, содержащей грань aa'b'b.
3. Соединив точки М и N, получим линию пересечения секущей плоскости и плоскости, содержащей грань abcd.
4. Проводим прямую da до пересечения с прямой MN в точке К. Точка К принадлежит секущей плоскости и плоскости, содержащей грань aa'd'd, следовательно, точки К и В принадлежат этим плоскостям и прямая, проведенная через точки К и В до пресечения с ребром a'd' в точке D даст нам линию пересечения секущей плоскости и плоскости, содержащей грань aa'd'd.
5. Соединив точки А,С,В и D получим искомое сечение.
P.S. Прямые MN и AD при точном построении будут параллельными, так как параллельные плоскости (верхняя и нижняя грани куба) секутся плоскостью сечения по параллельным прямым.