Предмет: Математика,
автор: lonlonpark10
Найдите S хакрашенного сегмента, если известно, что треугольник AOB прямоугольный и является четвёртой частью всей окружности
Приложения:
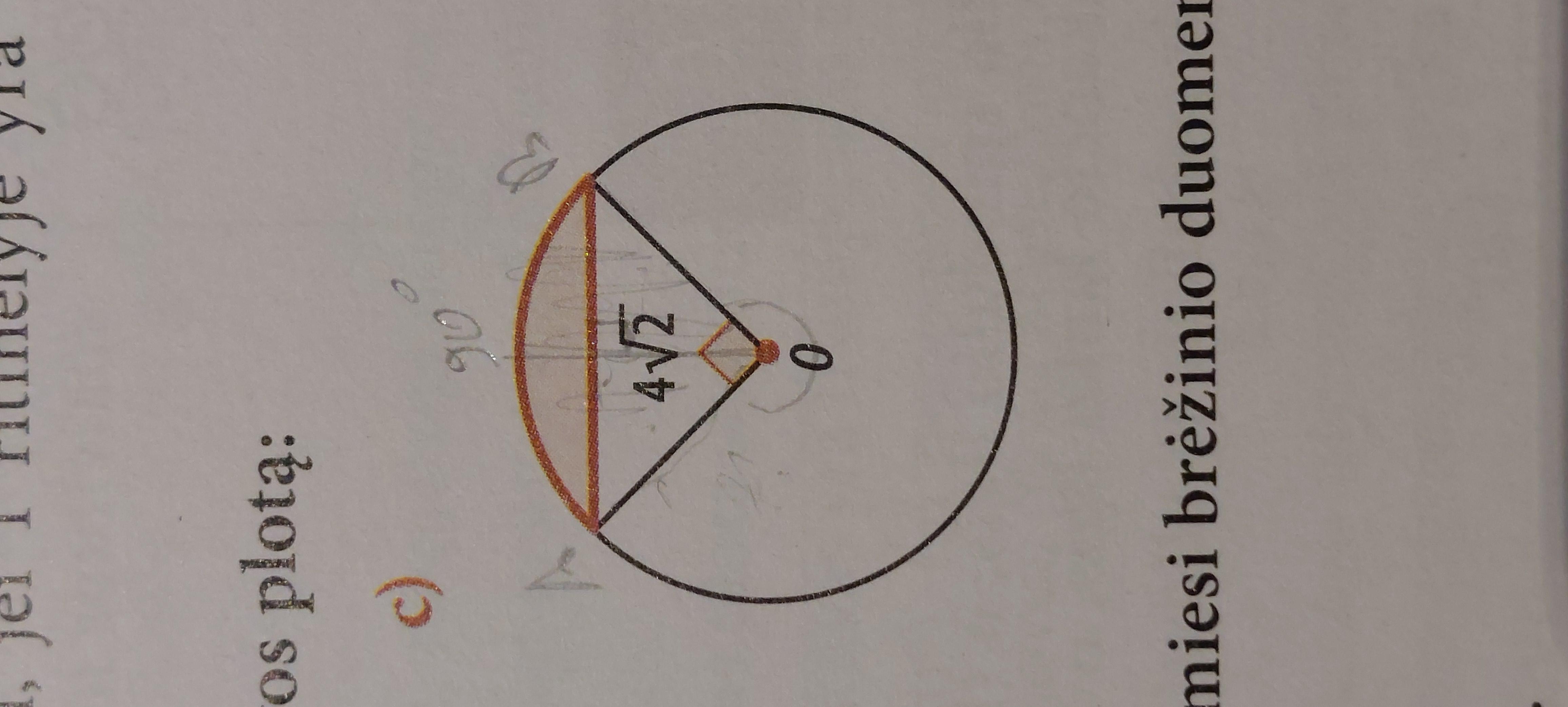
onetfriend:
1/4 площади круга минус площадь треугольника?
Для площади круга должен быть известен радиус, к сожалению, он не известен
а 4корня из 2 это к чему относится? что там вообще известно, кроме того что треугольник прямоугольный?
Ответы
Автор ответа:
0
Ответ:
32π - 4√2
Пошаговое объяснение:
Площадь треугольника равна половине произведения сторон на синус угла между ними.
Так как стороны АО = ОВ треугольника АОВ равны между собой как радиусы R окружности, а угол между ними равен 90°, то:
S AОВ = 4√2 = (R² · sin90°) : 2
8√2 = R² · 1
Откуда:
R = √128
Площадь S круга радиуса R равна:
S = πR² = π (√128)² = 128π
Соответственно 1/4 часть этой площади составляет:
128π : 4 = 32π,
а площадь Sc закрашенного сегмента:
Sc = 32π - 4√2
Ответ: 32π - 4√2
По теореме Пифагора я нашла R=2 корня из 3, после чего нашла S треугольника = 12, S сектора = корень из шести умноженное на пи и деленное на 2
S сег= S сёк ± S треуг
Если предположить, что R = 2√3, то тогда площадь исходного треугольника равна (2√3 х 2√3) : 2 = 4 х 3 : 2 = 12 : 2 = 6, что противоречит условию, согласно которому площадь треугольника равна 4√2. А если предположить, что 4√2 - это площадь 1/4 части круга, то тогда площадь круга = 16√2, откуда R² = 16√2/π, а площадь прямоугольника = 8√2/π. И тогда S сегм = 4√2 - 8√2/π = 4√2 ( 1 - 2/π).
Похожие вопросы
Предмет: Русский язык,
автор: 2008n
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Байрам228
Предмет: Алгебра,
автор: hdygb
Предмет: Другие предметы,
автор: katyagushchina