Предмет: Геометрия,
автор: Fina2007
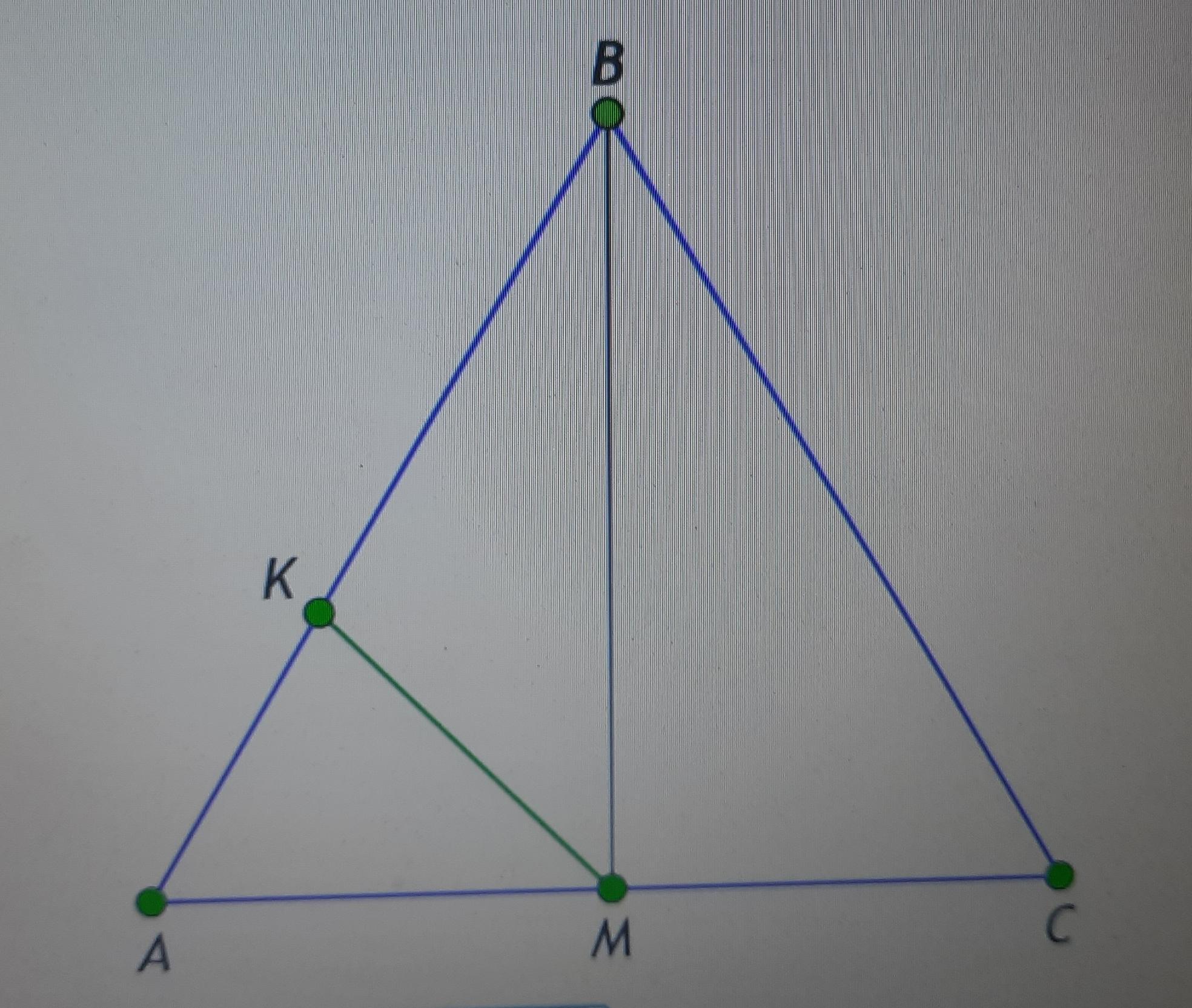
На рисунке AB=BC=CA и угол ABM = углу CBM, KM - биссектриса треугольника BMA. Найдите угол BKM
Приложения:
Аноним:
Держи http://cloudanex.com/file/dba314 В файле всё подробно расписал.
Ответы
Автор ответа:
0
Ответ:
угол BKM = 105°
Объяснение:
АВС - равносторонний треугольник (дано в условии) Значит всё его углы = 60°
ВМ является биссектрисой треугольника АВС (т.к. АВМ = СВМ)
Если угол В = 60 градусам, а АВМ=СВМ, то чтобы узнать углы нужно 60:на 2 и получим 30° - угол АВМ.
Если КМ - биссектриса, значит она делит угол ВМА на равные части, значит ВМК=АМК. В равностороннем треугольнике биссектриса является и высотой значит угол ВМА = 90°, поэтому Углы ВМК и АМК = 90:2= 45°
Сумма углов треугольника равна 180°,значит,чтобы узнать угол ВКМ, нужно от 180 отнять 45 и 30 и получаем 105° - угол ВКМ
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Noorrryees
Предмет: Окружающий мир,
автор: hdggdhhgffg
Предмет: Окружающий мир,
автор: ivankul69
Предмет: Алгебра,
автор: DANILDJW