Предмет: Геометрия,
автор: alexandr2000lad
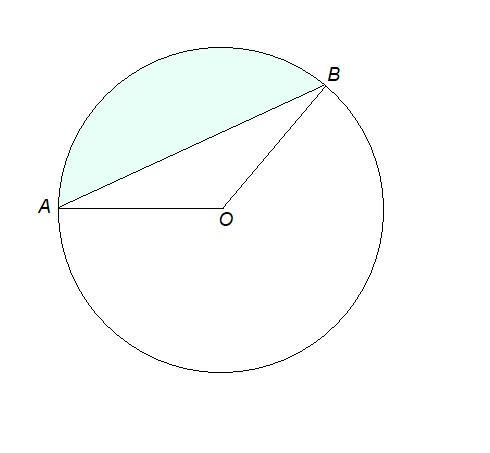
Найдите площадь сегмента, если радиус круга равен 18см, а радианная мера дуги, ограничивающей сегмент, равна 2π/3
Ответы
Автор ответа:
2
Ответ:
S = Sсект. - Sabc = (108 - 81√3) см²
Объяснение:
Чтобы найти площадь сегмента, надо из площади сектора вычесть площадь треугольника с вершинами в центре круга и на концах дуги, ограничивающей сегмент.
Радианная мера полной окружности равна 2π.
Тогда площадь сектора составляет треть площади круга.
Площадь круга:
Sкр. = πR² = π · 18² = 324π см²
Площадь сектора:
Sсект. = 324 : 3 = 108 см²
Градусная мера центрального угла ОАВ равна градусной мере дуги:
Площадь треугольника АОВ найдем как половину произведения двух сторон на синус угла между ними:
см²
Площадь сегмента:
S = Sсект. - Sabc = (108 - 81√3) см²
Приложения:
orjabinina:
S_{ABC}=\dfrac{1}{2}\cdot......?
помогите пожалуйста с геометрией
Похожие вопросы
Предмет: Русский язык,
автор: анна1594
Предмет: Русский язык,
автор: supersofik
Предмет: Окружающий мир,
автор: Panteraegovseva
Предмет: Физика,
автор: pushinaol
Предмет: История,
автор: tktjtgelrfjrhh