Question

Найдите длину окружности описанной около прямоугольного треугольника, периметр которого равен 28 см, а площадь равна 48 см².

Answer 1

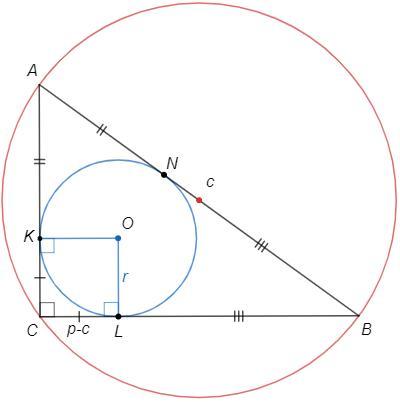
Рассмотрим любой треугольник и его вписанную окружность.

K L N - точки касания

Отрезки касательных из одной точки равны.

Видим три пары равных отрезков: AK=AN, BN=BL, CL=CK

Тогда AN+BN+CL =p (полупериметр) => CL=p-AB

(Аналогично AN=p-BC и т.д. Справедливо для любого треугольника.)

Теперь рассмотрим прямоугольный треугольник.

Проведем радиусы в точки касания на катетах.

Радиус в точку касания перпендикулярен касательной.

OKCL - прямоугольник с равными смежными сторонами - квадрат.

CK=CL=OK=OL =r

Oтрезок CL равен радиусу вписанной окружности.

Т.е. для прямоугольного треугольника справедливо

r =p-c (c - гипотенуза)

По формуле S =pr => r =S/p

c =p-r =p -S/p =14 -48/14 =74/7

Гипотенуза - диаметр описанной окружности прямоугольного треугольника.

L =74/7 п (см)  ~33,21

Разумеется, можно просто решить систему уравнений.

a+b+c =28 => a+b =28-c

ab/2 =48 => 2ab =192

a^2 +b^2 =c^2 (т Пифагора)

a^2 +b^2 +2ab =(a+b)^2

c^2 +192 =(28-c)^2 =28^2 -56c +c^2

c =(784-192)/56 =74/7