Предмет: Геометрия,
автор: sasalelikow07
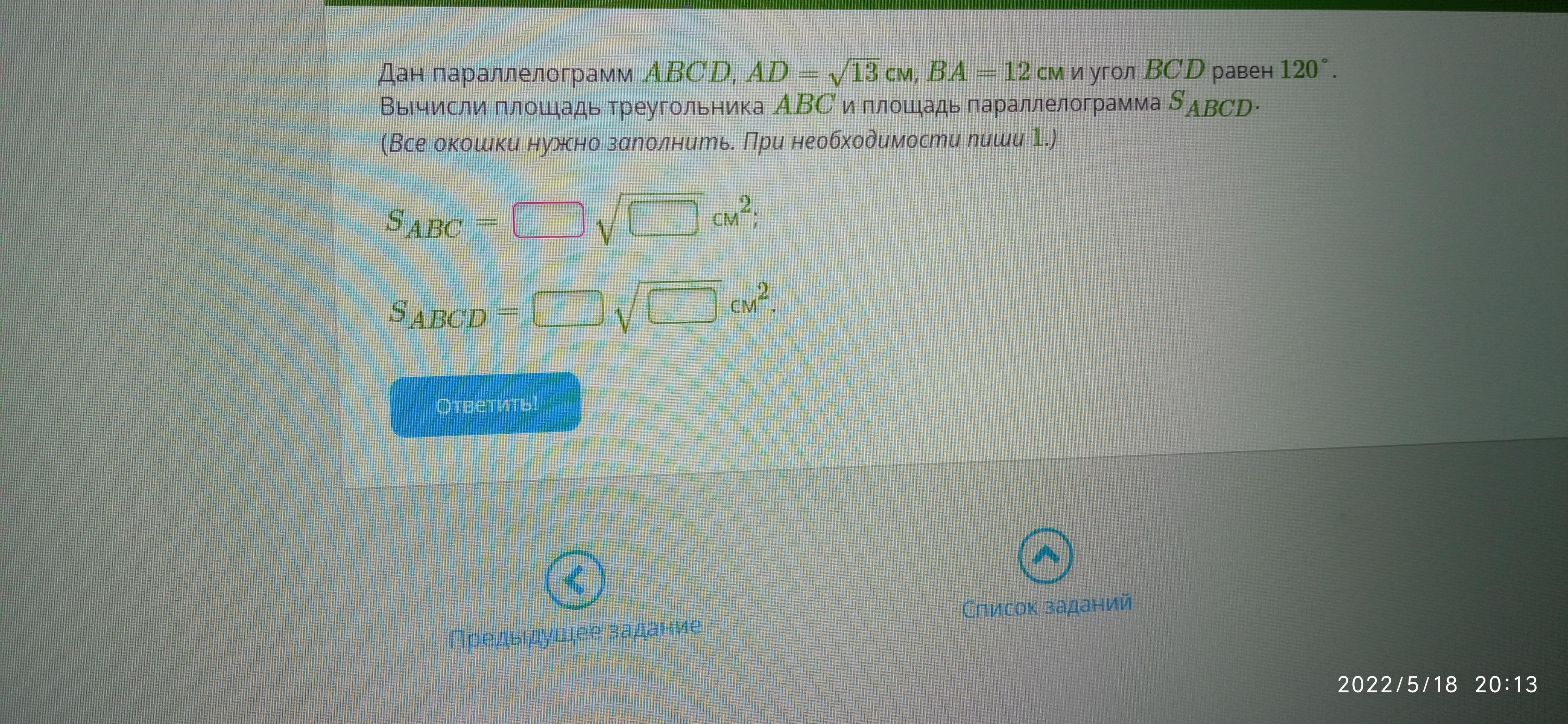
СРОЧНО даю 20 балов умоляю решите быстро
Приложения:
Ответы
Автор ответа:
0
Ответ:
см²
см²
Объяснение:
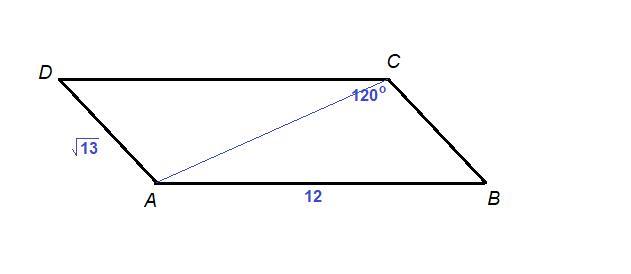
- Площадь параллелограмма равна произведению смежных сторон на синус угла между ними:
- Противоположные углы параллелограмма равны.
∠А = ∠С = 120°
см²
- Диагональ делит параллелограмм на два равных треугольника.
Тогда площадь треугольника АВС равна половине площади параллелограмма:
см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: maltsievaalina
Предмет: Русский язык,
автор: ЛИЗОК12345678910
Предмет: Математика,
автор: lilitaghadjanian
Предмет: История,
автор: rugayatagiyeva2007