Предмет: Геометрия,
автор: lijunni
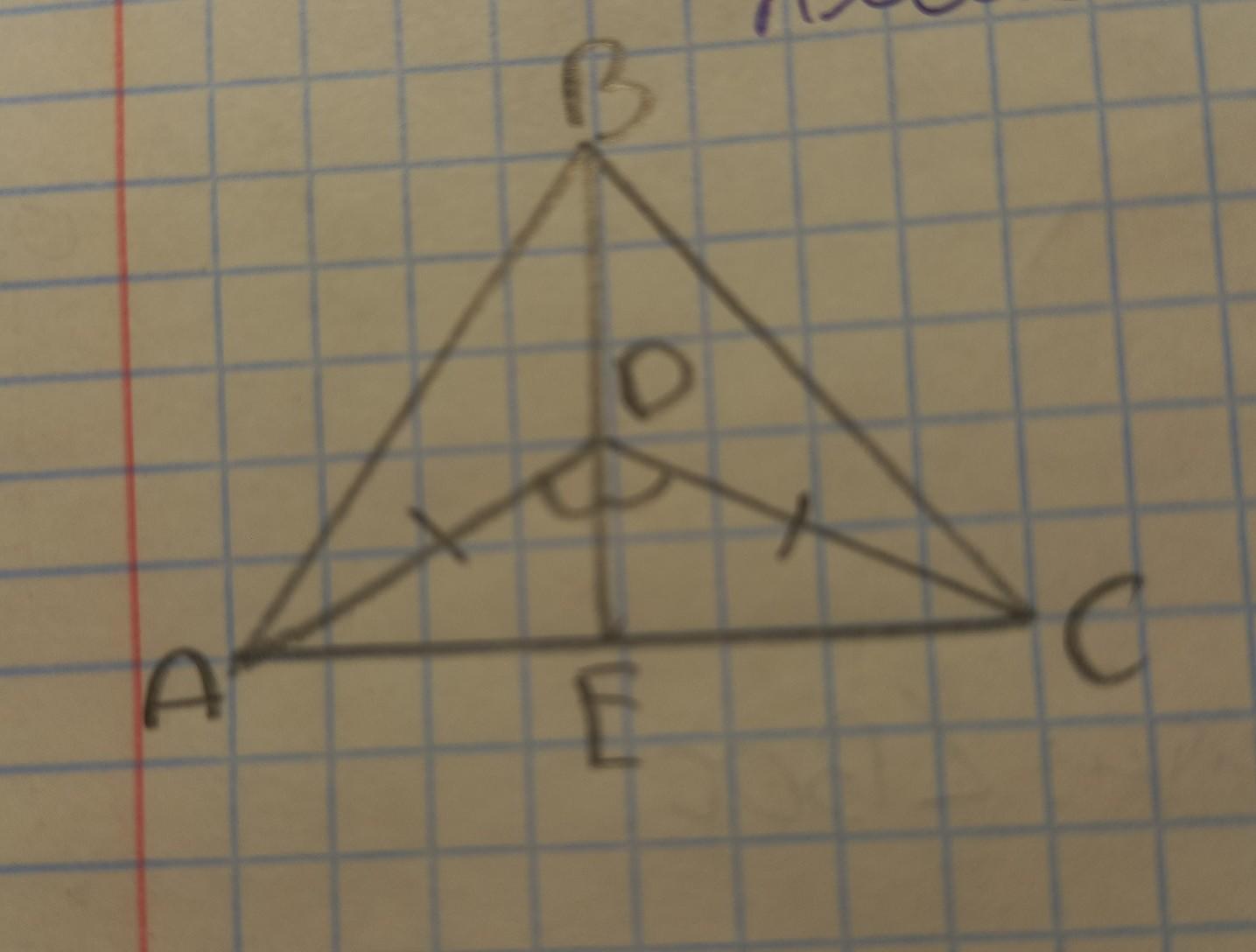
докажите что треугольник АБС равнобедренный.Помогите пожаалуйста!
Приложения:
Ответы
Автор ответа:
1
Доказательство:
ΔАОС равнобедренный, та как АО=СО, ОЕ - биссектриса угла О данного треугольника по условию. Следовательно, ОЕ не только биссектриса, но медиана и высота, то есть
АЕ = СЕ, а ОЕ⊥ АС
В ΔАВС отрезок ОЕ является частью отрезка ВЕ, следовательно, ВЕ высота ΔАВС. И, поскольку АЕ = СЕ, то ВЕ - медиана.
Известно, что если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный, что и требовалось доказать.
Похожие вопросы
Предмет: Русский язык,
автор: Дима200444
Предмет: Русский язык,
автор: dima617
Предмет: Русский язык,
автор: Qwerty197311
Предмет: Английский язык,
автор: masha2919