Question

Срочно!!!!Даю 100 баллов!!!!Основанием наклонной призмы является равнобедренный треугольник АВС, в котором АВ = АС = 10, ВС = 12. Вершина A1 равноудалена от вершин A, B и C и AA1 равна 13. Найти полную площадь поверхности этой призмы.Ответ 492, дайте пожалуйста понятное объяснение.​

Answer 1

Ответ:

Площадь полной поверхности 492 кв. ед.

Объяснение:

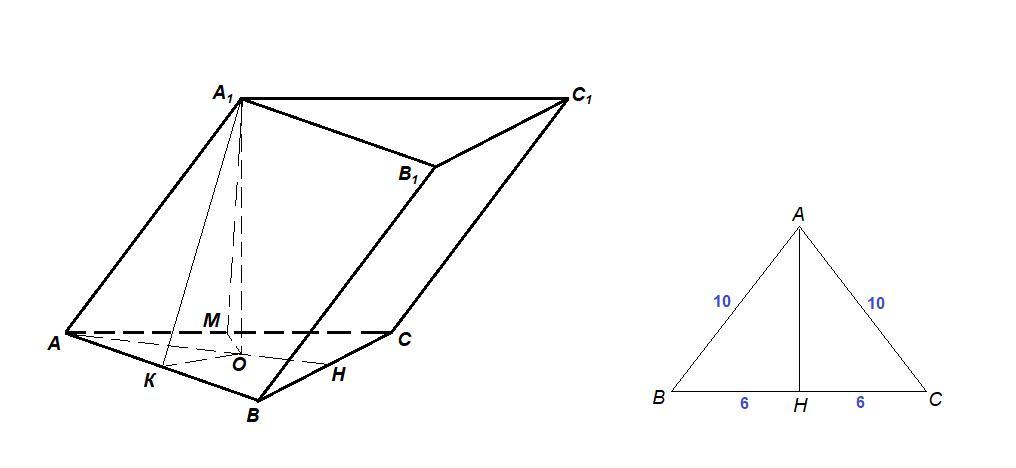
Так как вершина А₁ наклонной призмы равноудалена от вершин нижнего основания, то она проецируется в центр окружности, описанной около треугольника АВС, точку О.

• Центр окружности, описанной около треугольника, лежит в точке пересечения его серединных перпендикуляров.

Проведем АН - высоту (медиану) равнобедренного треугольника АВС. О лежит на ВН.

Пусть К и М середины сторон АВ и АС треугольника АВС соответственно. Тогда ОК и ОМ - серединные перпендикуляры к этим сторонам.

ОК и ОМ - проекции наклонных А₁К и А₁М, значит

А₁К⊥АВ и А₁М⊥АС по теореме о трех перпендикулярах.

ΔА₁АК = ΔА₁АМ по гипотенузе и катету:

• ∠А₁КА = ∠А₁МА = 90°;
• АА₁ - общая гипотенуза;
• АК = АМ как половины равных сторон.

Тогда А₁К = А₁М, и площади граней АА₁В₁В и АА₁С₁С равны (равны высоты и стороны, к которым они проведены).

Из прямоугольного треугольника А₁АК по теореме Пифагора:

А₁К = √(АА₁² - АК²)

АК = 0,5 АВ = 0,5 · 10 = 5

А₁К = √(13² - 5²) = √(169 - 25) = √144 = 12

$S_{AA_1B_1B}=AB\cdot A_1K=10\cdot 12=120$

$\boldsymbol{S_{AA_1C_1C}=S_{AA_1B_1B}=120}$

АО⊥ВС (АО лежит на АН), АО - проекция АА₁ на (АВС), значит АА₁⊥ВС по теореме о трех перпендикулярах.

Так как боковые ребра призмы равны и параллельны, то

ВВ₁⊥ВС, то есть ВВ₁С₁С - прямоугольник.

$\boldsymbol{S_{BB_1C_1C}}=BB_1\cdot BC=13\cdot 12\boldsymbol{=156}$

Для нахождения площади треугольника АВС найдем его высоту по теореме Пифагора:

AH = √(АВ² - ВН²) = √(10² - 6²) = √(100 - 36) = √64 = 8

$\boldsymbol{S_{ABC}}=\dfrac{1}{2}BC\cdot AH=\dfrac{1}{2}\cdot 12\cdot 8\boldsymbol{=48}$

Площади оснований равны.

Площадь полной поверхности:

$S=2S_{AA_1C_1C}+S_{BB_1C_1C}+2S_{ABC}$

S = 2 · 120 + 156 + 2 · 48 = 240 + 156 + 96 = 492