Предмет: Математика,
автор: Аноним
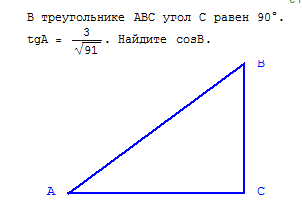
В треугольнике ABC угол С равен 90- градусов
(Во вложения).....
Приложения:
Ответы
Автор ответа:
0
cos B=BC/AB sin A=BC/AB отсюда cos B=sin A


косинус находим через другую тригонам.формулу



подставляем значение косинуса в квадрате в формулу


так как cos B=sin A , то
косинус находим через другую тригонам.формулу
подставляем значение косинуса в квадрате в формулу
так как cos B=sin A , то
Автор ответа:
0
заметим В+A=90
B=90-A
cos B = cos 90-A=sin A
известен tg A
tg²A=1/cos²A-1
9/91+1=1/cos²A
так как косинус и синус меньше 90 то они положительные
сos²A=91/100
sinA=√1-cos²A=√1-91/100=√9/100=3/10
cosB=SinA=3/10
B=90-A
cos B = cos 90-A=sin A
известен tg A
tg²A=1/cos²A-1
9/91+1=1/cos²A
так как косинус и синус меньше 90 то они положительные
сos²A=91/100
sinA=√1-cos²A=√1-91/100=√9/100=3/10
cosB=SinA=3/10
Похожие вопросы
Предмет: Русский язык,
автор: dasha2003061
Предмет: Русский язык,
автор: МаркМус
Предмет: Русский язык,
автор: coneIloveyou
Предмет: Математика,
автор: oteofilova