Предмет: Геометрия,
автор: kozacukalinka17
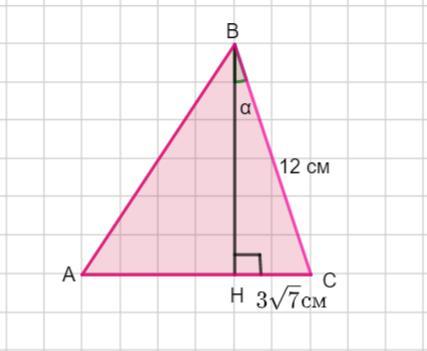
У трикутнику АВС: ВН- висота, кут АВС= 30 градусів, ВС= 12 см, СН= 3 корені з 7 см. Знайти довжину АН
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Пусть дан Δ АВС , ∠АВС = 30°, ВС =12 см, проведена высота ВН . СН= 3√7 см .
Рассмотрим треугольник Δ ВНС - прямоугольный , так как ВН- высота. Применим теорему Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Обозначим в данном треугольнике ∠СВН через α.
Тогда ∠АВН= 30°-α.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Рассмотрим Δ АНВ - прямоугольный.
Воспользуемся формулой тангенса разности:
Тогда получим
Найдем длину отрезка АН
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: SegeyStrakatov1
Предмет: Русский язык,
автор: Ретклифф
Предмет: Русский язык,
автор: mariacool1
Предмет: Геометрия,
автор: www6969
Предмет: Математика,
автор: turdiyevam