Question

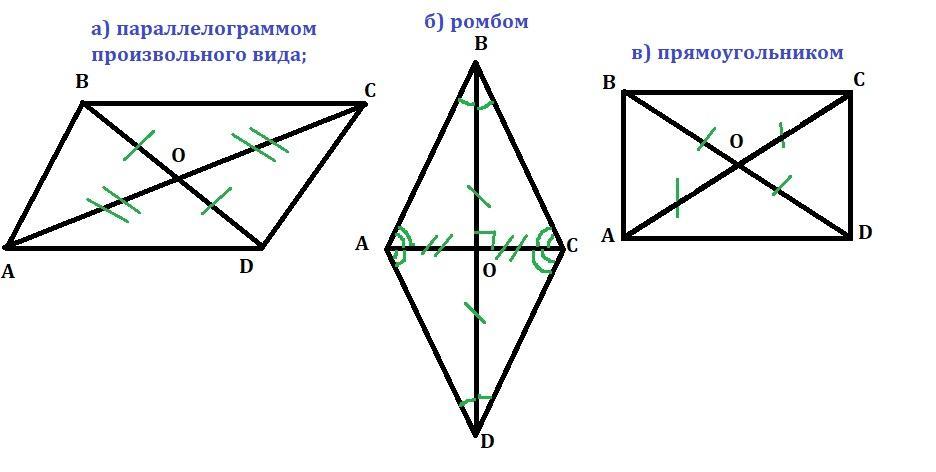
Диагонали четырёхугольника ABCD пересекаются в точке O. Укажите верные утверждения для каждого из случаев, когда четырёхугольник ABCD ЯВЛЯЕТСЯ:
а) параллелограммом произвольного вида;
б) ромбом
в) прямоугольником

Answer 1

Ответ:

Объяснение:

Диагонали четырёхугольника ABCD пересекаются в точке O. Укажите верные утверждения для каждого из случаев, когда четырёхугольник ABCD ЯВЛЯЕТСЯ:

а) параллелограммом произвольного вида;

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства параллелограмма:

• В параллелограмме противоположные стороны равны

AB=CD, ВС=AD.

• В параллелограмме противоположные  углы равны.

∠ABC = ∠ADC, ∠BAD = ∠BCD

• В параллелограмме точка пересечения диагоналей делит их пополам.

BO=OD, AO=OC.

б) ромбом

Ромб — параллелограмм, у которого все стороны равны.

Свойства ромба:

а) Все свойства параллелограмма:

• В ромбе противоположные стороны равны

AB=CD, ВС=AD.

• В ромбе противоположные  углы равны.

∠ABC = ∠ADC, ∠BAD = ∠BCD

• В ромбе точка пересечения диагоналей делит их пополам.

BO=OD, AO=OC.

б) + свойства ромба:

• Все стороны равны

AB=BC=CD=AD

• Диагонали ромба пересекаются под прямым углом  

AC ⊥ BD, ⇒ AO⊥BO

• Диагонали ромба являются биссектрисами его углов.

∠DCA = ∠BCA, ∠ABО = ∠CBО, ∠BAO=∠DAO, ∠ADO=∠CDO.

в) прямоугольником

Прямоугольником называется параллелограмм, у которого все углы прямые

Свойства прямоугольника:

а) Все свойства параллелограмма:

• В прямоугольнике противоположные стороны равны

AB=CD, ВС=AD.

• В прямоугольнике противоположные  углы равны.

∠ABC = ∠ADC, ∠BAD = ∠BCD

• В прямоугольнике точка пересечения диагоналей делит их пополам.

BO=OD, AO=OC.

б) + свойства прямоугольника:

• Диагонали прямоугольника равны.

AC=BD, BO=OD=AO=OC

• Все углы прямоугольника - прямые

∠АВС = ∠BCD = ∠CDA = ∠DAB = 90°

#SPJ1