Question

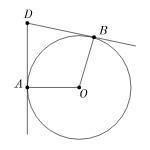
Через точки A и B окружности с центром в точке O проведены две касательные AD и BD . Градусная мера меньшей дуги AB равна 116 градусов . Найди угол ADB . Ответ дай в градусах

Answer 1

Ответ:

Угол ADB равен 64°.

Объяснение:

Через точки A и B окружности с центром в точке O проведены две касательные AD и BD . Градусная мера меньшей дуги AB равна 116 градусов . Найди угол ADB .

Дано: Окр.О;

AD и BD - касательные;

◡АВ = 116°

Найти: ∠ADB

Решение:

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ∠DAO = 90°; ∠DBO = 90°.

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ∠АОВ = ◡АВ = 116° (центральный)

• Сумма углов четырехугольника равна 360°.

⇒ ∠ADB = 360° - (∠DAO + ∠DBO + ∠АОВ) =

= 360° - (90° + 90° + 116°) = 64°

Угол ADB равен 64°.

#SPJ1