помогите...........
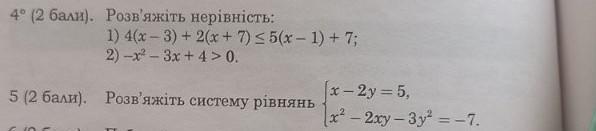
Ответы
Ответ:
В решении.
Объяснение:
4.
1) 4(х - 3) + 2(х + 7) <= 5(х - 1) + 7
Раскрыть скобки:
4х - 12 + 2х + 14 <= 5х - 5 + 7
Привести подобные:
6х + 2 <= 5х + 2
6х - 5х <= 2 - 2
х <= 0
Решения неравенства: х∈(-∞; 0].
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда под круглой скобкой.
2) -х² - 3х + 4 > 0
Приравнять к нулю и решить квадратное уравнение:
-х² - 3х + 4 = 0/-1
х² + 3х - 4 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 9 + 16 = 25 √D=5
х₁=(-b-√D)/2a
х₁=(-3-5)/2
х₁= -8/2
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-3+5)/2
х₂=2/2
х₂= 1;
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х= -4 и х= 1.
у > 0 (парабола выше оси Ох) при х от х= -4 до х= 1.
Решения неравенства: х∈(-4; 1).
Неравенство строгое, скобки круглые.
5. (способ подстановки);
х - 2у = 5
х² - 2ху - 3у² = -7
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 5 + 2у
(5 + 2у)² - 2у(5 + 2у) - 3у² = -7
Раскрыть скобки:
25 + 20у + 4у² - 10у - 4у² - 3у² = -7
Привести подобные:
-3у² + 10у + 32 = 0/-1
3у² - 10у - 32 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 100 + 384 = 484 √D=22
у₁=(-b-√D)/2a
у₁=(10-22)/6
у₁= -12/6
у₁= -2;
у₂=(-b+√D)/2a
у₂=(10+22)/6
у₂=32/6
у₂= 16/3 (дробь);
Теперь вычислить х:
х = 5 + 2у
а) х₁ = 5 + 2 * (-2)
х₁ = 5 - 4
х₁ = 1;
б) х₂ = 5 + 2 * 16/3
х₂ = 5 + 32/3
х₂ = 47/3;
Решения системы уравнений: (1; -2); (47/3; 16/3).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.