Предмет: Математика,
автор: zpe89577
СРОЧНО ПЖ!!!!
Объем продукции U, произведенной предприятием в течение рабочего дня, задан функцией U=U(t),  , где t – рабочее время, час. Найти:
, где t – рабочее время, час. Найти:
1) производительность труда (уже нашел  )
)
2) при каком значении t после начала работы производительность труда является максимальной.
Нужно пошаговое решение!!
Приложения:
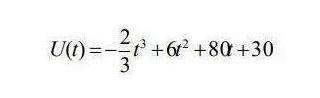
Ответы
Автор ответа:
1
Ответ:
1) производительность труда р(t) = -2t² +12t -80
2) производительность труда является максимальной при t = 3
Пошаговое объяснение:
1) Производительность труда - это фактически скорость, т.е. количество произведенной продукции в час.
Скорость - это первая производная от, в данном случае, объема продукции
2) Чтобы найти экстремум функции p(t) = -2t² +12t -80 возьмем производную и приравняем ее к нулю
p'(t) =( -2t² +12t -80)' = -4t +12
-4t +12 = 0
t = 3
Можно считать по другому.
p(t) = -2t² +12t -80 - это парабола, ветвями вниз. Максимума достигает в вершине параболы. Значение абсциссы вершины параболы ищется по формуле
Похожие вопросы
Предмет: Қазақ тiлi,
автор: hova1
Предмет: Қазақ тiлi,
автор: hova1
Предмет: Английский язык,
автор: DiamondEng
Предмет: Математика,
автор: 0394
Предмет: Английский язык,
автор: koko347