Question

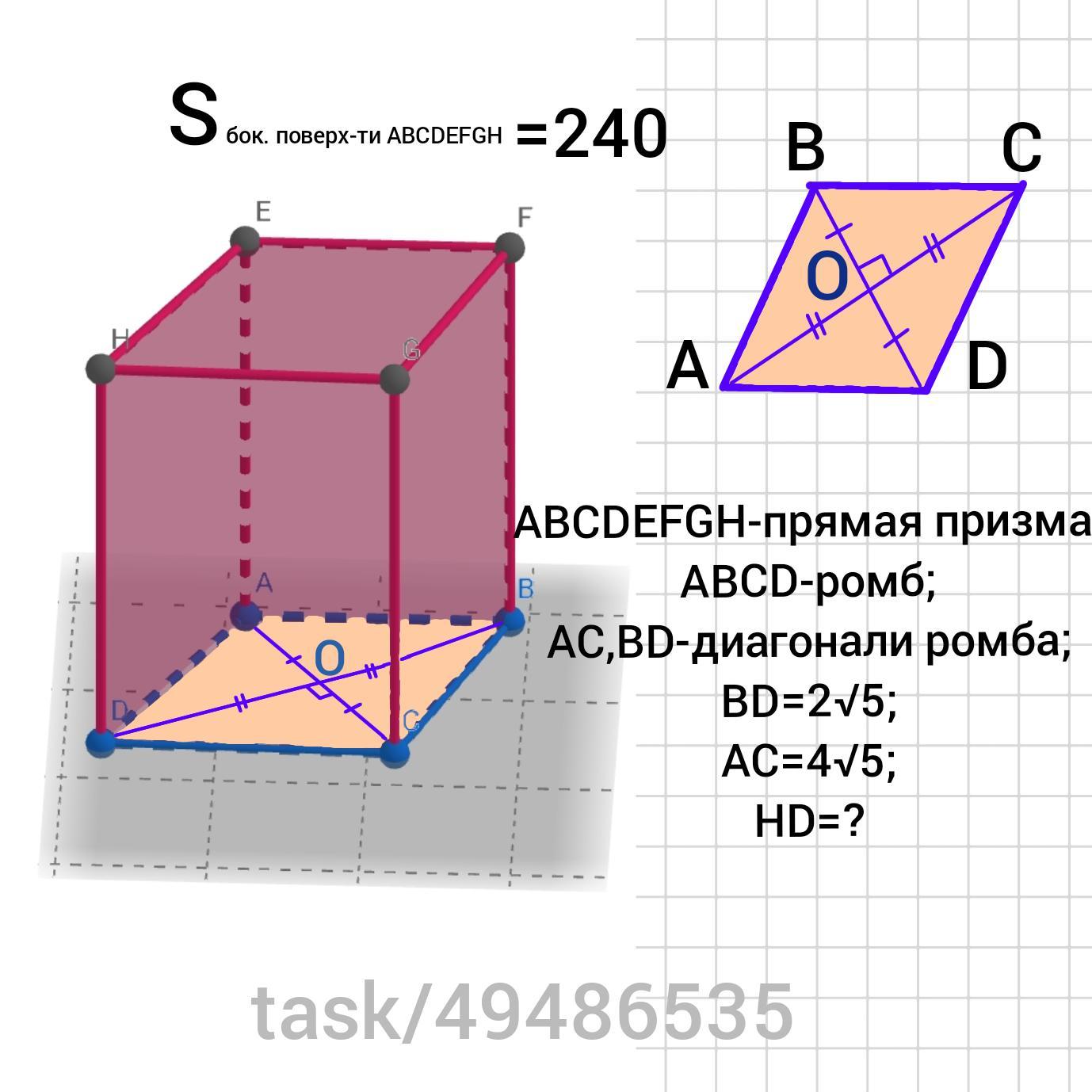
В основании прямой призмы лежит ромбо диагоналями 2√5 и 4√5. Найди боковое ребро этой призмы, если её площадь боковой поверхности равна 240.​

Answer 1

Ответ:

$12$

Объяснение:

• найдем периметр основания призмы-в данном случае это ромб; диагоналями он разделен на четыре равных между собой прямоугольных треугольника, воспользуемся теоремой Пифагора, чтобы найти гипотенузу ($AD$,к примеру): $\displaystyle AD^2=AO^2+OD^2;\\\\\displaystyle AD^2=\bigg(\frac{AC}{2} \bigg)^2+\bigg(\frac{BD}{2} \bigg)^2;\\\\\displaystyle AD^2=\bigg(\frac{4\sqrt{5} }{2} \bigg)^2+\bigg(\frac{2\sqrt{5} }{2} \bigg)^2;\\\\\displaystyle AD=\sqrt{(2\sqrt{5})^2+(\sqrt{5} )^2 } =\sqrt{25} =5;$ периметр ромба-сумма всех его сторон,следовательно,$P_{ABCD}=AD*4=5*4=20;$
• чтобы найти площадь боковой поверхности призмы,нужно вычислить произведение периметра ее основания и высоты (у прямой призмы высота совпадает с боковым ребром). выразим  длину бокового ребра из этой формулы и вычислим его:

$S_b=P_{ABCD}*HD;\\\\\displaystyle HD=\frac{S_b}{P_{ABCD}} =\frac{240}{20} =12$