Предмет: Алгебра,
автор: awpretard
6. Упростите выражение: (5y ^ 2)/(1 - y ^ 2) / (1 - 1/(1 - y)) b)( x xy-y^ 2 - y x^ 2 -xy ): x^ 2 -y^ 2 8xy
Приложения:
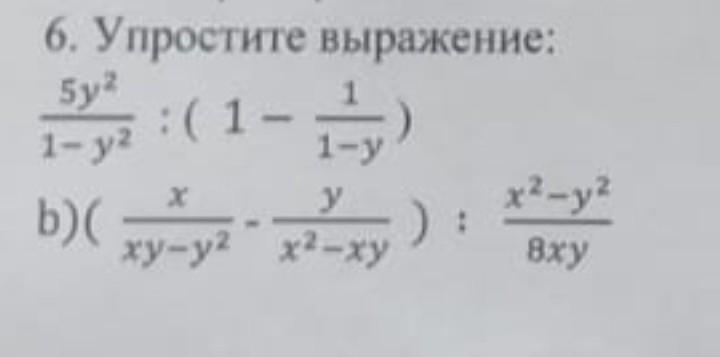
Ответы
Автор ответа:
7
ответ:
решение:
Похожие вопросы
Предмет: Английский язык,
автор: drtrgj
Предмет: Русский язык,
автор: Chloe7300
Предмет: Қазақ тiлi,
автор: baurdzhan
Предмет: Українська мова,
автор: nazarkostenuk475