ТЕОРІЯ ЙМОВІРНОСТЕЙ
Знайти закон розподілу дискретної випадкової величини х, яка може набувати тільки два значення: х(1) з ймовірністю p=0.5 і х(2), причому х(1) < х(2) Математичне сподівання M(x)=4; дисперсія D(x)= 4.
Ответы
M(x) = p(x1)*x1+p(x2)*x2=0,5*x1+0,5*x2=4
D(x) = M( (x-M(x) )²) = p(x1)*(x1-4)² + p(x2)*(x2-4)²=0,5*(x1-4)² + 0,5*(x2-4)² = 4
********************
x1+x2=8
(x1-4)² + (x2-4)² = 8
*****************
x1=8-x2
(4-x2)² + (x2-4)² = 8
****************
x1=8-x2
(x2-4)² = 4=2²
****************
x2-4=2; x2=6; x1=8-x2=8-6=2
или
x2-4=-2; x2=2; x1=8-x2=8-2=6 - не підходить бо за умовою х(1) < х(2)
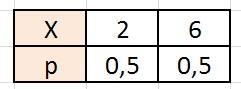
закон розподілу дискретної випадкової величини х
X=
{ 2; p=0,5}
{ 6; p=0,5}
Ответ:
Пошаговое объяснение:
Найти закон распределения дискретной случайной величины X, которая может принимать только два значения: X₁ с вероятностью p₁ = 0,5 и X₂, причем X₁ < X₂. Математическое ожидание M(X)=4; дисперсия D(X)=4.
Поскольку
p₁ + p₂ = 1
то p₂ = 1 - 0,5 = 0,5
1)
Математическое ожидание:
X₁·p₁ +X₂·p₂ = M(X)
X₁·0,5 +X₂·0,5 = 4
Получили первое уравнение системы:
0,5·(X₁ + X₂) = 4
X₁ + X₂ = 8 (1)
2)
Учтем, что и величина дисперсии известна. Тогда вычисляем:
X₁²·p₁ +X₂²·p₂ = M(X²)
0,5 (X₁² +X₂²) = M(X²)
D(X) = M(X²) - [M(X)]²
4 = 0,5 (X₁² +X₂²) - 4²
0,5 (X₁² +X₂²) = 4² + 4
X₁² + X₂² = 40 (2)
Решим систему уравнений:
Решая эту систему,получаем:
X₁ = 2
X₂ = 6
Закон распределения дискретной случайной величины: