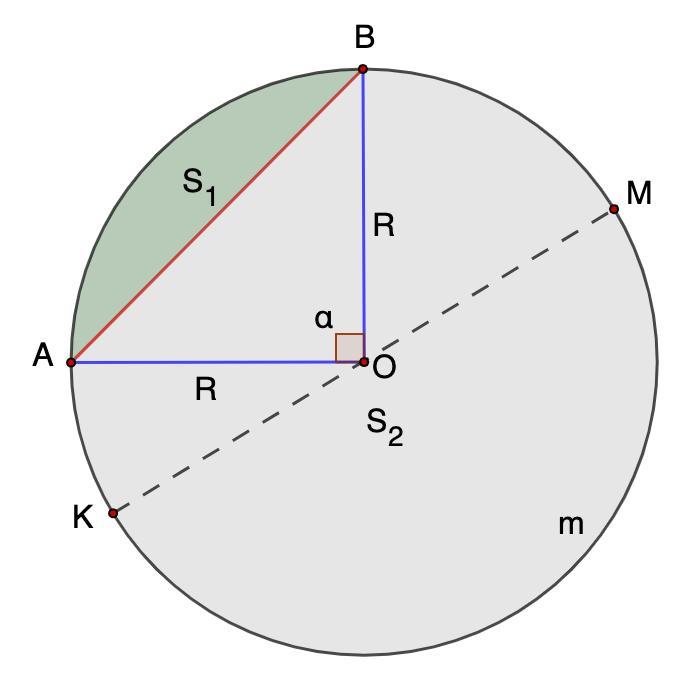
Кінці хорди ділять коло у відношенні 1:3. Знайди площі двох утворених сегментів, якщо діаметр кола дорівнює 24 см.
Ответы
Ответ:
Площади сегментов равны:
S₁ = (36π - 72) см² ≈ 41,04 см²;
S₂ = (108π +72) см² ≈ 411,12 см².
Объяснение:
Концы хорды делят окружность в отношении 1:3. Найди площади двух образованных сегментов, если диаметр окружности равен 24 см.
Дано: Окр.О,R;
AB - хорда;
◡АВ : ◡AmB = 1 : 3
КМ = 24 см - диаметр.
Найти: площади сегментов S₁ и S₂.
Решение:
◡АВ : ◡AmB = 1 : 3
- Градусная мера окружности равна 360°.
Пусть ◡АВ = х°: тогда ◡AmB = 3х°
Составим уравнение:
х + 3х = 360°
х = 90°
◡АВ = 90°: ◡AmB = 270°
- Центральный угол равен градусной мере дуги, на которую он опирается.
⇒ α = 90°
- Радиус равен половине диаметра.
⇒ R = KM : 2 = 12 см.
- Площадь прямоугольного треугольника равна половине произведения катетов.
Знаем α, R и S(AOB).
Площадь меньшего сегмента S₁ найдем по формуле.
Найдем площадь меньшего сегмента S₁:
Площадь большего сегмента S₂ найдем по формуле:
Здесь α = 270°.
Подставим значения и найдем площадь сегмента S₂:
Площади сегментов равны:
S₁ = (36π - 72) см² ≈ 41,04 см²;
S₂ = (108π +72) см² ≈ 411,12 см².
#SPJ1