Предмет: Алгебра,
автор: ssevda2005
Определи значение выражения

Ответы
Автор ответа:
2
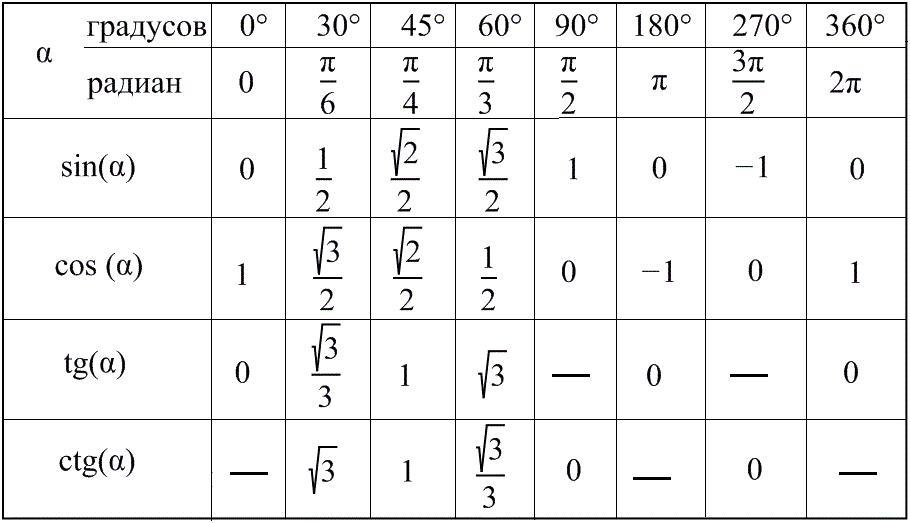
Найти значение выражения sin²2π - cos²(-π/2) + sin²(-3π/2).
Ответ:
Значение выражения равно единице.
Объяснение:
К ответу прикрепляю таблицу значений sin a и cos a при разных значениях а.
cos(-x)=cos x, sin(-x)=(-sin x).
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Tfissergay1
Предмет: Русский язык,
автор: nohacknocheat
Предмет: Английский язык,
автор: thestese
Предмет: Русский язык,
автор: gd380
Предмет: Английский язык,
автор: OnlineGill