Предмет: Алгебра,
автор: naninani242405
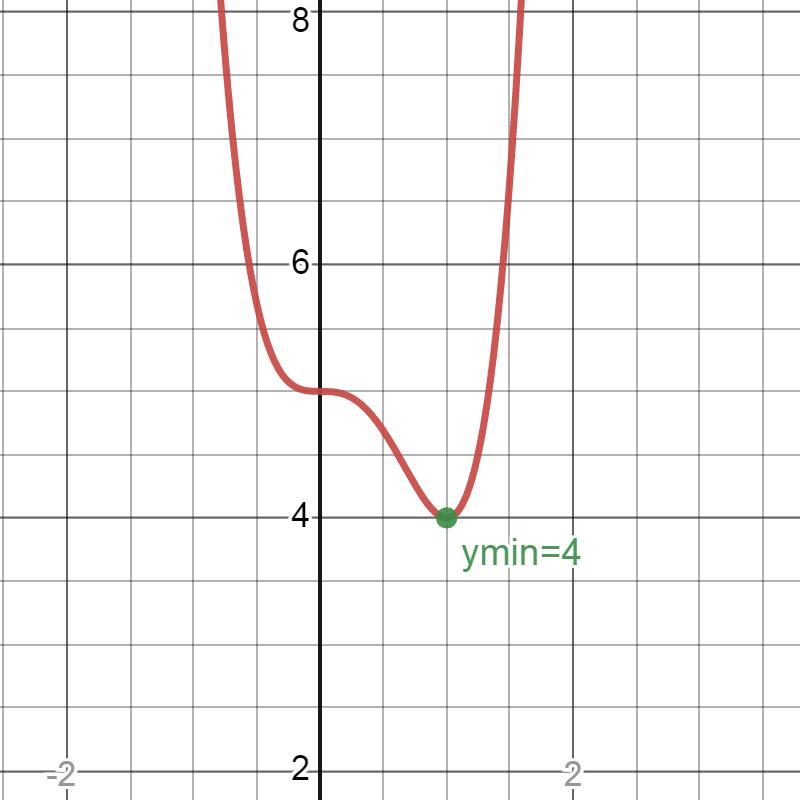
Найти min функции y=3x4-4x3+5 на интервале [-2;3]
Ответы
Автор ответа:
1
Объяснение:
Ответ: ymin=y(1)=4.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: pipkina1973
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Алексей298706
Предмет: Физика,
автор: sestunovaula632
Предмет: Математика,
автор: nasiba8278