Предмет: Алгебра,
автор: novyjokaunt
3 реши неравенство методом интервалов
Приложения:
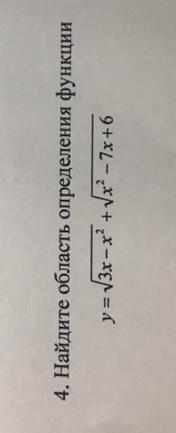
Ответы
Автор ответа:
1
Объяснение:
ОДЗ:
x*(x-3)≤0
-∞__+__0__-__3__+__+∞ ⇒
x∈[0;3].
(x-6)*(x+1)≥0
-∞__+__-1__-__6__+__+∞ ⇒
x∈(-∞;-1]U[6;+∞)
Система неравенств не имеет решений ⇒
Ответ: х∈∅.
novyjokaunt:
Спасибо большое
Удачи.
Похожие вопросы
Предмет: Другие предметы,
автор: nikitakorochink
Предмет: Русский язык,
автор: oles2001
Предмет: Русский язык,
автор: ваасыфы
Предмет: Химия,
автор: listil12
Предмет: География,
автор: Аноним