Предмет: Алгебра,
автор: Zalunko
СРОЧНО!!!!!!!!!!!!!!!!!!!!!!!!!!.
Приложения:

Ответы
Автор ответа:
0
Ответ:
a) y=4+0²
y=4
y=4+2²
y=8
b) y=2-(-2)
y=4
y=2-1
y=1
в) y=4•(-1) ³+1
y=-3
y=4•2³+1
y=33
Автор ответа:
0
Объяснение:
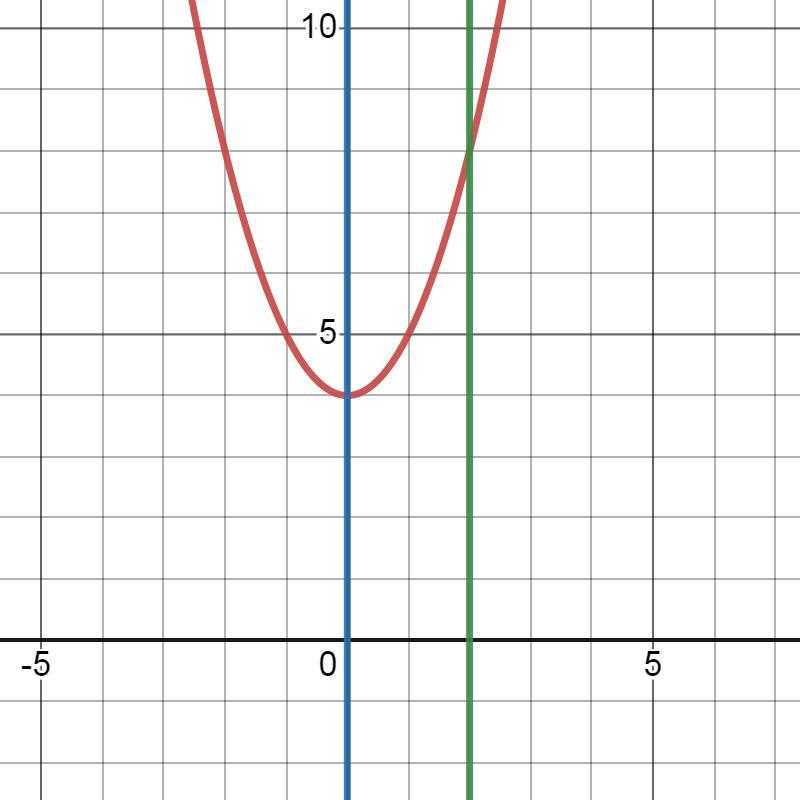
а)
Ответ: S≈10,66667 кв.ед.
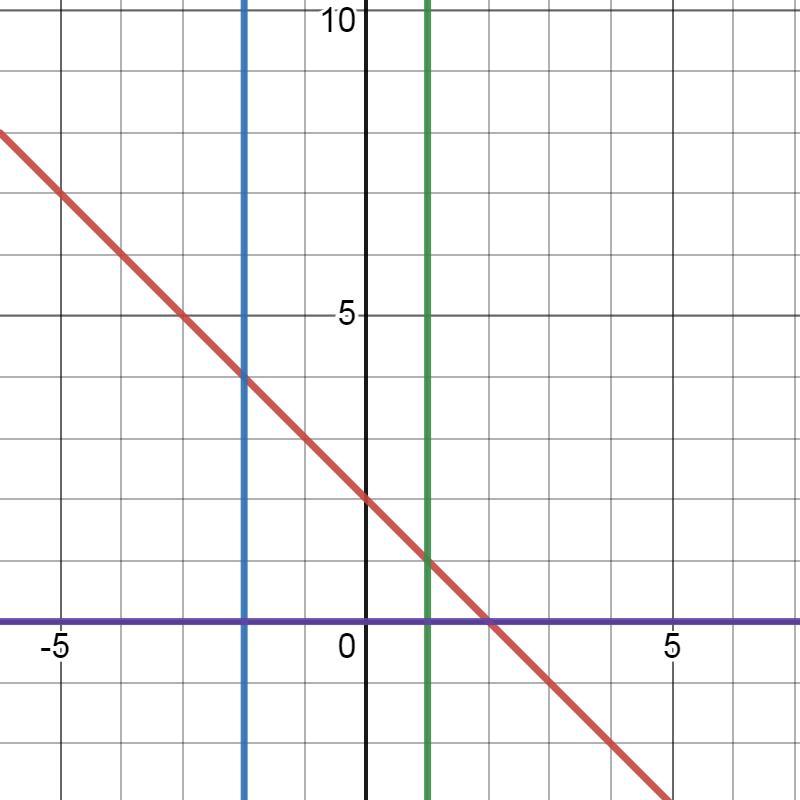
б)
Ответ: S=7,5 кв.ед.
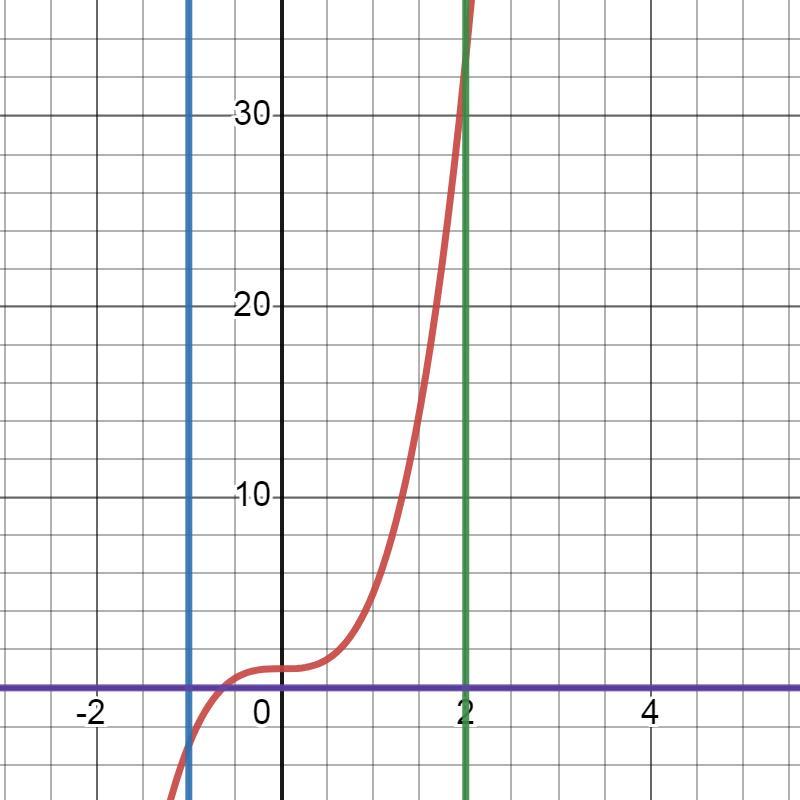
в)
Ответ: S=18 кв.ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: lvygsgc
Предмет: Русский язык,
автор: Щенок101
Предмет: Русский язык,
автор: рукоделие1
Предмет: Английский язык,
автор: mira080645
Предмет: Алгебра,
автор: loyll