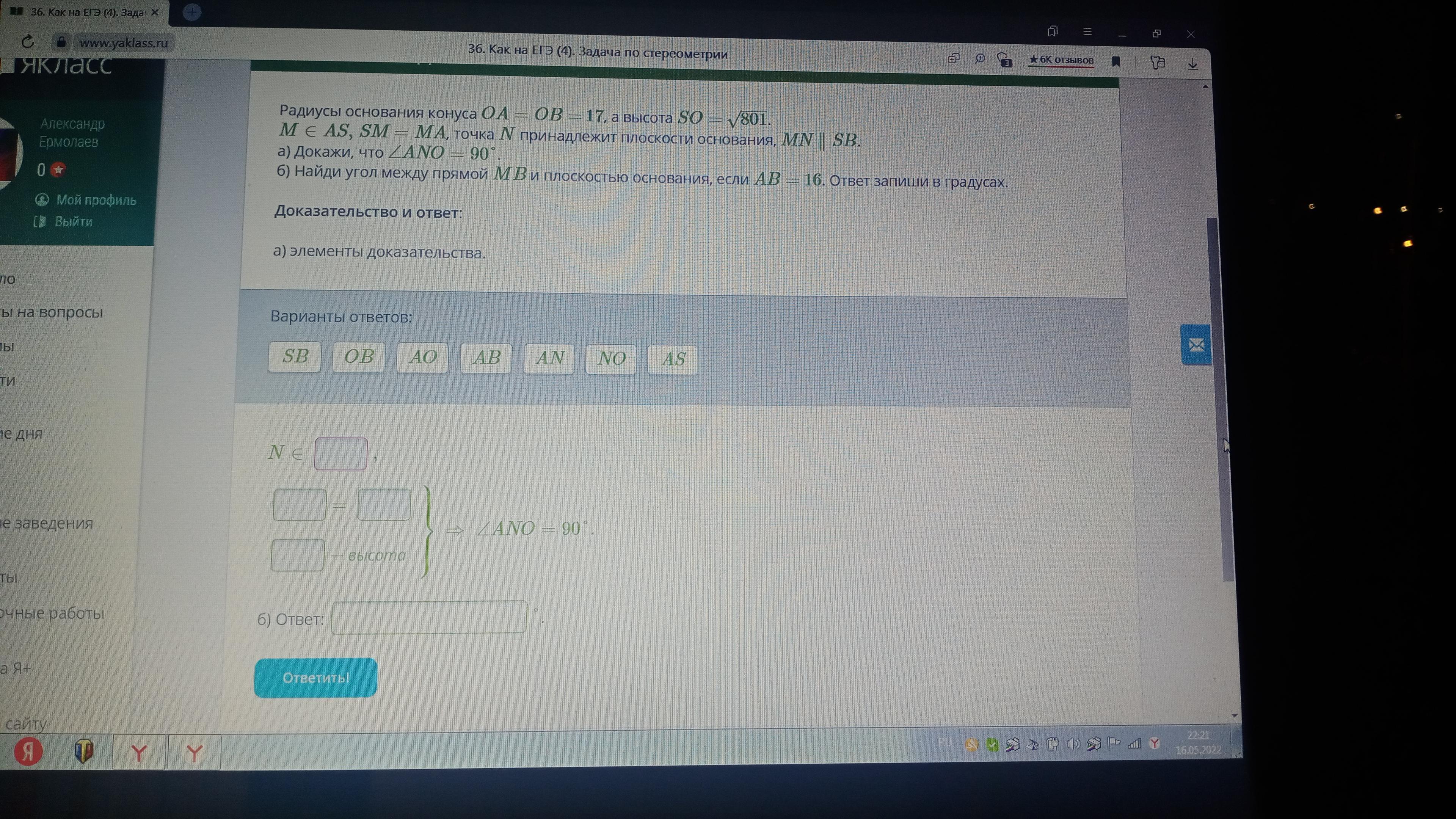
Радиусы основания конуса OA=OB=17, а высота SO=√801
M (принадлежит) AS, SM=MA, Точка N принадлежит плоскости основания, MN ll SB
а) Докажите , что угол ANO=90°
б) Найди угол между прямой MB и плоскостью основания, если AB=16 Ответ запишите в градусах
1. Чему равна высота
2. Точка N принадлежит
Ответы
a) Через параллельные MN и SB проходит плоскость. Эта плоскость пересекает основание по прямой, все общие точки плоскостей принадлежат этой прямой. Точка A лежит на прямой SM, следовательно в плоскости параллельных и следовательно на общей прямой. A-N-B на одной прямой.
MN||SB, AM=MS => AN=NB (т Фалеса)
△AOB - равнобедренный. ON - медиана к основанию, следовательно и высота, ∠ANO=90°.
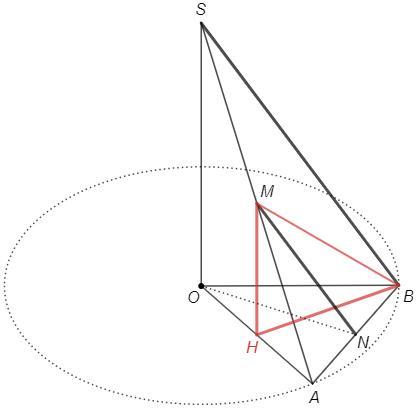
б) Опустим перпендикуляр MH на основание. OA - проекция наклонной SA, следовательно точка H упадет на OA.
Угол между прямой и плоскостью - угол между прямой и ее проекцией. ∠MBH - искомый.
SO||MH, AM=MS => MH - средняя линия в △SAO (по признаку)
MH =SO/2 =√801/2
BH - медиана в △AOB
BH =√(2(AB^2+OB^2)-OA^2)/2 =√(2*16^2 +2*17^2 -17^2)/2 =√801/2
tg(MBH) =MH/BH =1 => ∠MBH=45°
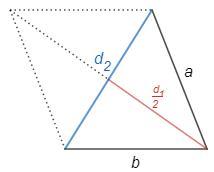
d₁^2 +d₂^2 =2(a^2 +b^2) => d₁/2 =√(2(a^2 +b^2) -d₂^2)/2