Предмет: Алгебра,
автор: anelayam101
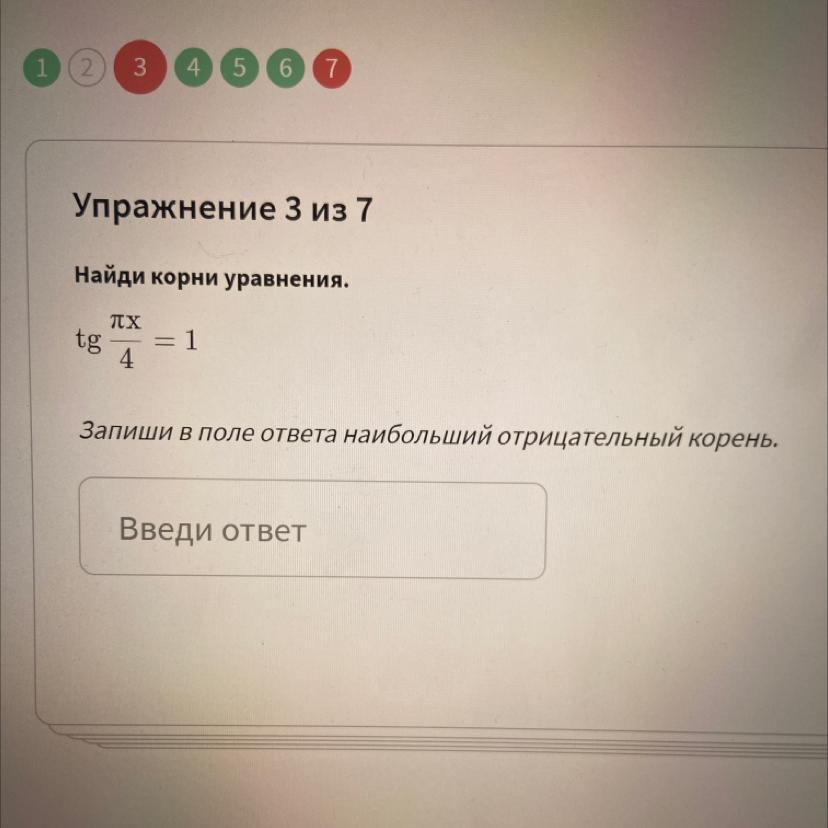
Найди корни уравнения 10-й класс. Помогите пожалуйста
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
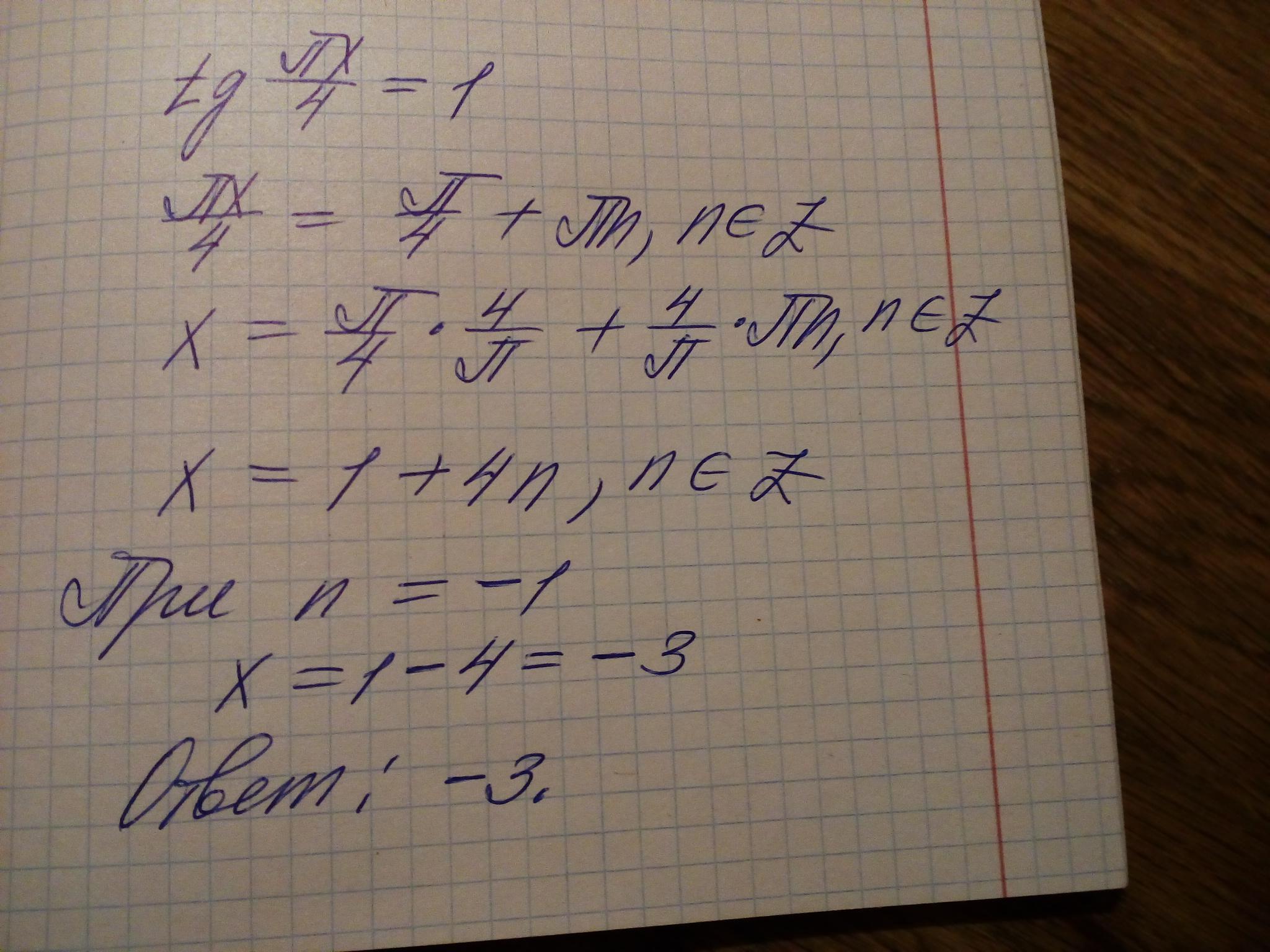
Автор ответа:
2
Найти корни уравнения tg (πx/4)=1 и записать наибольший отрицательный корень.
Ответ:
Решение уравнения: x=1+4n, n ∈ Z; наибольший отрицательный корень уравнения х=(-3).
Объяснение:
Формула для решения уравнения вида tg x = b:
Если tg x = b, то x=arctg b + πn, n ∈ Z.
Применяем её в нашем уравнении:
Найдём наибольший отрицательный корень (x<0). Для этого рассмотрим разные варианты значений n.
При уменьшении n корни будут также уменьшаться, соответственно, продолжать поиски не имеет смысла. Наибольший корень, который соответствует условию x<0 - x=(-3).
Похожие вопросы
Предмет: Русский язык,
автор: вода01
Предмет: Қазақ тiлi,
автор: avdkirill
Предмет: Английский язык,
автор: MiLA909715
Предмет: Алгебра,
автор: Аноним
Предмет: Русский язык,
автор: rinatmuss