Question

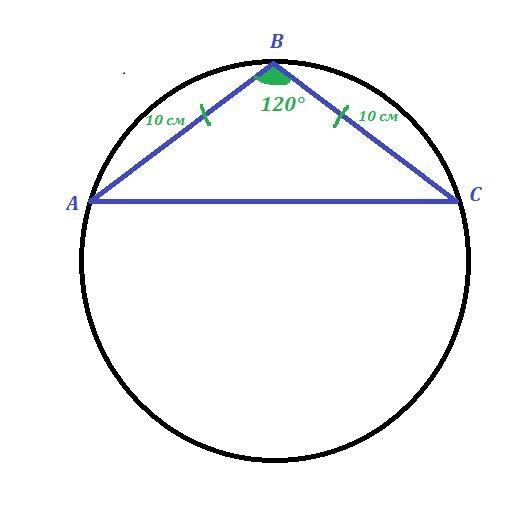
В равнобедренном треугольнике ABC с основание AC и боковой стороной, равной 10, угол B = 120градусов. Найдите диаметр окружности, описаной около треугольника АВС

Answer 1

Ответ:

Диаметр окружности, описанной около треугольника АВС равен 20 см

Объяснение:

В равнобедренном треугольнике ABC с основание AC и боковой стороной, равной 10, ∠B = 120° .

Найдите диаметр окружности, описаной около треугольника АВС.

• Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.

• В равнобедренном треугольнике углы при основании равны.

• Расширенная теорема синусов:

Для произвольного треугольника стороны треугольника пропорциональны синусам противолежащих углов и равны удвоенному радиусу окружности, описанной вокруг треугольника.

$\dfrac{a}{sin\alpha } =\dfrac{b}{sin\beta } =\dfrac{c}{sin \gamma} =2R$

Где a, b, c - стороны треугольника,

$\alpha , \beta , \gamma$ - соответственно противолежащие им углы,

R - радиус окружности, описанной вокруг треугольника.

Известно, что 2R=D.

Найдём D - диаметр окружности.

Решение

Так как ΔАВС - равнобедренный, то

∠А=∠С=(180°-∠В):2=(180°-120°):2=30°.

Согласно расширенной теореме синусов:

$D=\dfrac{BC}{sin30^\circ} =\dfrac{10}{\frac{1}{2} } = 20 CM$

Диаметр окружности, описанной около треугольника АВС равен 20 см

#SPJ1