Question

ДАЮ 30 балів
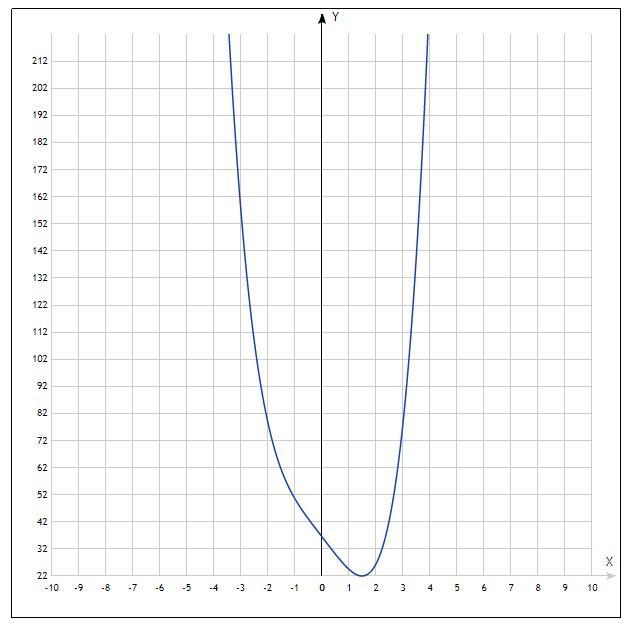
Дослідити функцію f(x)= х 4 -13х+36 і побудувати її графік.

Answer 1

$f(x) = x^4 -13x+36$

1. Область визначення.

x є (-∞;+∞).

2. Перевірка на парність.

$y(x)=x^4 -13x+36\\y(-x)=(-x)^4-13(-x)+36=x^4 +13x+36\\y(x)\neq y(-x)\\y(x)\neq -y(x)$

Функція ні парна, ні непарна.

3. Точки перетину графіку функцій з віссю координат.

Знайдемо точки перетину з віссю ординат Oy, тому прирівнюємо x до 0:

$y=0^4-13*0+36=36.$

Таким чином, точка перетину з віссю Oy має координати (0; 36).

Знайдемо точки перетину з віссю абсцис Ox, для цього прирівнюємо y до 0:

$x^4-13x+36=0$

Рівняння не має коренів, тому точок перетину з віссю Ox немає.

4. Аналіз функції на екстремум і монотонність.

$f'(x)=(x^4-13x+36)'=4x^3-13.\\4x^3-13=0\\x=\frac{\sqrt[3]{26} }{2} .$

                _                   +

--------------------($\frac{\sqrt[3]{26} }{2}$)---------------------------

спадає                     зростає                

 f'(x)<0                        f'(x)>0

В точці x = $\frac{\sqrt[3]{26} }{2}$ похідна функції змінює знак з (-) на (+). Отже, точка x = $\frac{\sqrt[3]{26} }{2}$ – точка локального мінімуму.

$f(\frac{\sqrt[3]{26} }{2} )=(\frac{\sqrt[3]{26} }{2} )^4-13(\frac{\sqrt[3]{26} }{2} )+36=-\frac{39\sqrt[3]{26} }{8} .$

Точка мінімуму: $(\frac{\sqrt[3]{26} }{2}; -\frac{39\sqrt[3]{26} }{8} ).$

5. Дослід на вгнутість та опуклість функції.

$f''(x)=(4x^3-13)'=12x^2.\\12x^2=0\\x^2=0\\x=0.$

         +                             +

--------------------($0$)---------------------------            

     f''(x)>0                      f'(x)>0

            функція вгнута.

6. Асимптоти.

$\lim_{x \to +\infty} (x^4 -13x+36)=$+∞.

значить, горизонтальних асимптот немає.

За визначення асимптоти:

$\lim_{x \to \infty} (kx+b-f(x))$

Тепер знаходимо коефіцієнт К:

$k= \lim_{x \to \infty} (\frac{f(x)}{x} )= \lim_{x \to \infty} \frac{x^4 -13x+36}{x} =$ ∞.

якщо k=∞  => нахилених асимптот немає.