Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
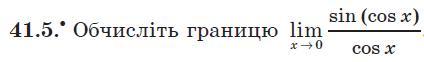
Ответы
Автор ответа:
2
Ответ:
Предел:
Примечание:
--------------------------------------------------------------
если
в точке
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: мих81
Предмет: Английский язык,
автор: ЕвгенияВайсберг
Предмет: Русский язык,
автор: вдв2235
Предмет: Қазақ тiлi,
автор: spiderlive12
Предмет: Химия,
автор: GrGzGm