Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
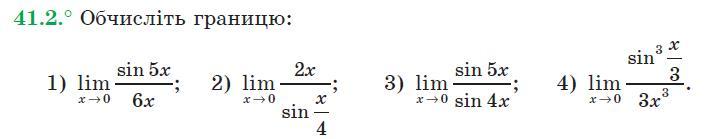
Ответы
Автор ответа:
1
Ответ:
Пределы:
1)
2)
3)
4)
Примечание:
Первый замечательный предел:
Следствие из первого замечательного предела:
при условии, что
--------------------------------------------------------------------
если
в точке
Теоремы: (при условии, что имеют предел в точке
)
Предел суммы:
Предел произведения:
Следствие из предела произведения:
Предел частного:
при условии, что
Объяснение:
1)
2)
3)
4)
Похожие вопросы
Предмет: Другие предметы,
автор: Alex2108
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: vladislav3972vlad
Предмет: Математика,
автор: lam2005