Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:

Ответы
Автор ответа:
2
Ответ:
1)
2)
3)
4)
5)
6)
Примечание:
если
Объяснения:
1)
2)
3)
4)
Примеры 5) и 6) смотрите на фотографии!!!
Приложения:
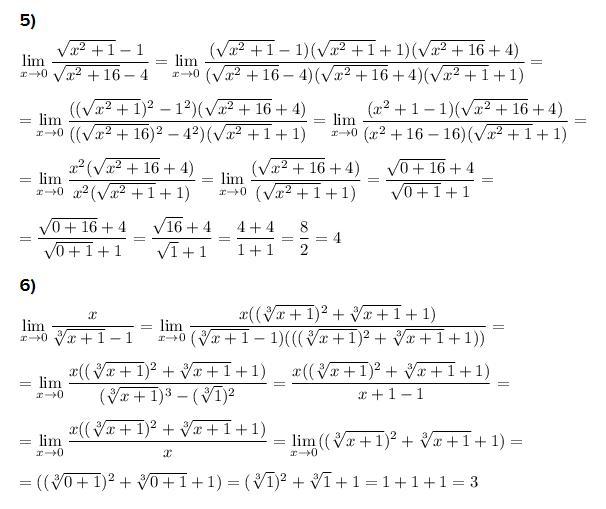
kimmina7373:
здравствуйте вы не могли бы мне помочь с алгеброй пожалуйста умоляю
Похожие вопросы
Предмет: Русский язык,
автор: катя2788
Предмет: Русский язык,
автор: knopik121
Предмет: Английский язык,
автор: 1Чупакабра1
Предмет: Обществознание,
автор: Alinakhut
Предмет: Алгебра,
автор: Saidka2005Vasya