Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
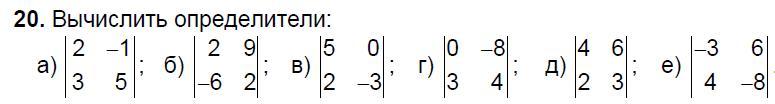
Ответы
Автор ответа:
1
Ответ:
Определители:
а)
б)
в)
г)
д)
е)
Примечание:
Формула для вычисления определителя матрицы A размером 2 на 2 в общем виде:
- определитель матрицы
Объяснение:
а)
б)
в)
г)
д)
е)
Похожие вопросы
Предмет: Русский язык,
автор: 2ешнuк
Предмет: Қазақ тiлi,
автор: goisaanna
Предмет: Русский язык,
автор: Naberezhneva
Предмет: Окружающий мир,
автор: penkova74
Предмет: Алгебра,
автор: marinakova04