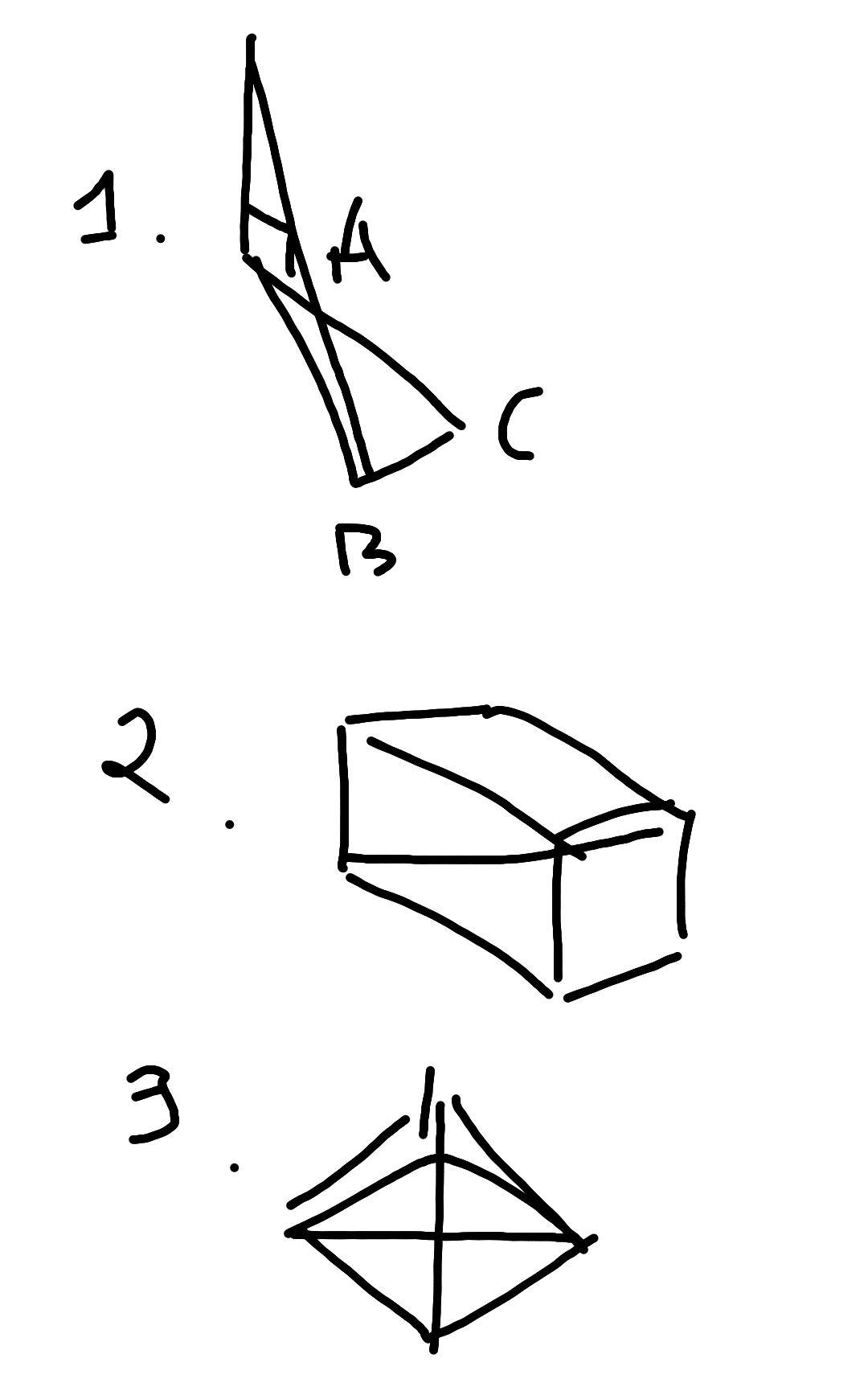
1. Дан прямоугольный треугольник АВС с гипотенузой АС = 13 см и катетом ВС = 5 см. Отрезок РA — перпендикуляр к плоскости АВС, равный 12 см. Найдите угол между прямой РB и плоскостью АВС.
2. В прямоугольном параллелепипеде длина диагонали 4√21 см, длины его измерений относятся как 1: 2 : 4. Найти площадь полной поверхности параллелепипеда.
3. В правильной четырехугольной пирамиде диагональ основания равна 4√3 см, а двугранный угол при основании равен 60°. Найдите площадь полной поверхности пирамиды.
Ответы
Ответ:
В прямоугольном параллелепипеде длина диагонали 4√21 см, длины его измерений относятся как 1: 2 : 4. Найти площадь полной поверхности параллелепипеда.
Объяснение:
Ответ:
1) Находим 2 катет:
За Пифагоровой пирамидой - 12 см
РА = АВ, как видно, поэтому треугольник АРВ - прямоугольный равнобедренный, а значит у него два угла по 45° каждый.
Ответ: 45°
2) Пускай х - одна из сторон параллелипипеда
Поверхность у такого параллелепипеда S = ( 4x • 2x ) • 2 + ( 4x • x ) • 2 + ( 2x • x ) • 2 =
16x² + 8x² + 4x² = 28x²
За теоремой Пифагора:
Диагональ нижней плоскости² = 16х² + 4х²
Диагональ н. п.² = 20х²
Дальше выходит, что:
(4√21)² = х² + 20х²
336 = 21х²
х² = 16
х = 4
Подставляем в нашу формулу поверхности:
S = 28x² = 28 • 16 = 448 см²
Ответ: 448 см²
3) Угол при основании - 60°, это правильная пирамида - значит его треугольные стены - равносторонние
Находим за теоремой Пифагора сторону квадратного основания через диагональ:
2а² = (4√3)², где а - сторона квадрата
2а² = 48
а² = 24
а = √24 или 2√6
S поверхность = Sквадр + 4 • Sтреуг
Sквадр = а² = 24 см²
Sтреуг = 1/2а • h = √6 • √18 = √108 см²
( Ps: h находим через Пифагора, 24 - 6 = 18, значит h = √18 см)
S поверх = 24 + 4√108 = (24 + 6√3) см²
Ответ: (24 + 6√3) см²
Объяснение: