Question

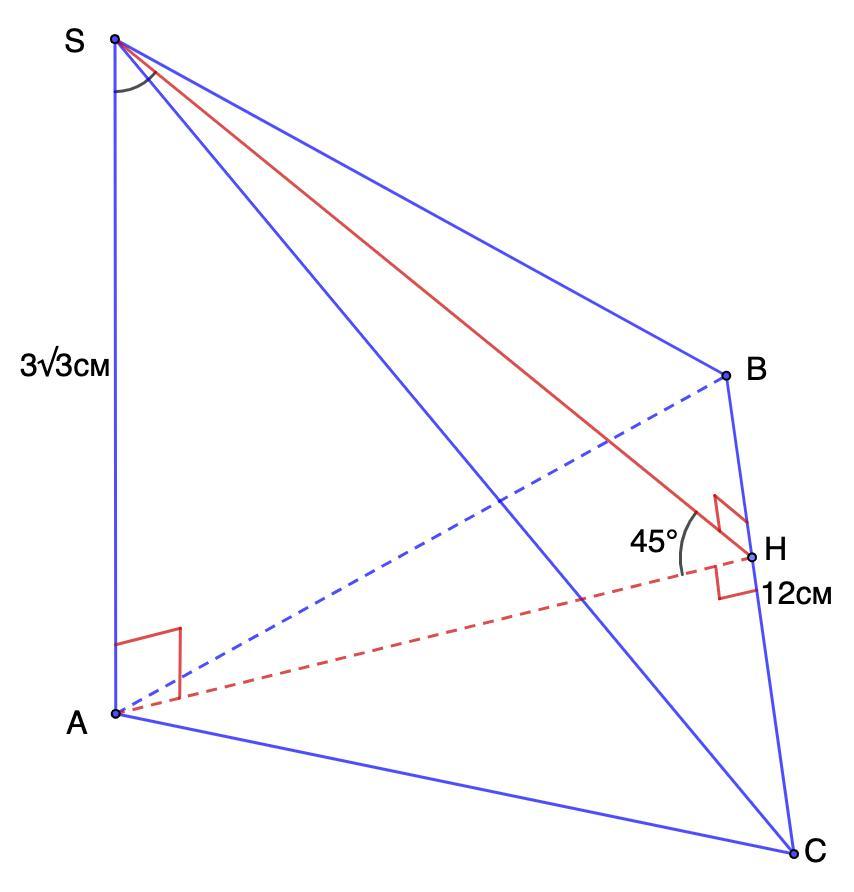
SABC - пирамида. SA перпендикулярен (ABC), SA=3√3 см ,BC=12см, двугранный угол при ребре BC равен 45 градусов . Выполнив рисунок, вычислите объем пирамиды.

Answer 1

Ответ:

Объем пирамиды равен 54 см³.

Объяснение:

SABC - пирамида. SA перпендикулярен (ABC), SA=3√3 см, BC=12 см, двугранный угол при ребре BC равен 45 градусов . Выполнив рисунок, вычислите объем пирамиды.

Дано: SABC - пирамида;

SA ⊥ АВС;

SA=3√3 см, BC=12 см;

Двугранный угол при ребре BC = 45°.

Найти: V(SABC)

Решение:

Объем пирамиды найдем по формуле:

$\displaystyle \boxed { V=\frac{1}{3}SH }$ , где S - площадь основания; Н - высота пирамиды.

Высота пирамиды SA=3√3 см.

Надо найти площадь основания.

1. Рассмотрим ΔASH.

• Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, принадлежащей этой плоскости.

⇒ ΔASH - прямоугольный.

• Двугранный угол между двумя плоскостями измеряется линейным углом, образованным двумя лучами, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.

АН ⊥ СВ

• Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

⇒ HS ⊥ CB.

⇒ ∠SHA = 45° - линейный угол двугранного угла SBCA.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ASH = 90° - ∠SHA = 90° - 45° = 45°

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ ΔASH - равнобедренный.

AS = AH = 3√3 см.

2. Рассмотрим ΔАВС.

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

ВС = 12 см; AH = 3√3 см.

$\displaystyle S(ABC)=\frac{1}{2}\cdot{CB} \cdot{AH}=\frac{1}{2}\cdot12\cdot3\sqrt{3} =18\sqrt{3} \;_{(CM)}$

3. Найдем объем пирамиды:

$\displaystyle V(SABC)=\frac{1}{3} S(ABC)\cdot{SA}=\frac{1}{3}\cdot 18\sqrt{3}\cdot3\sqrt{3}= 54\;_{(CM^3)}$

Объем пирамиды равен 54 см³.

#SPJ1