Предмет: Математика,
автор: solka0000
ВИЩА МАТЕМАТИКА
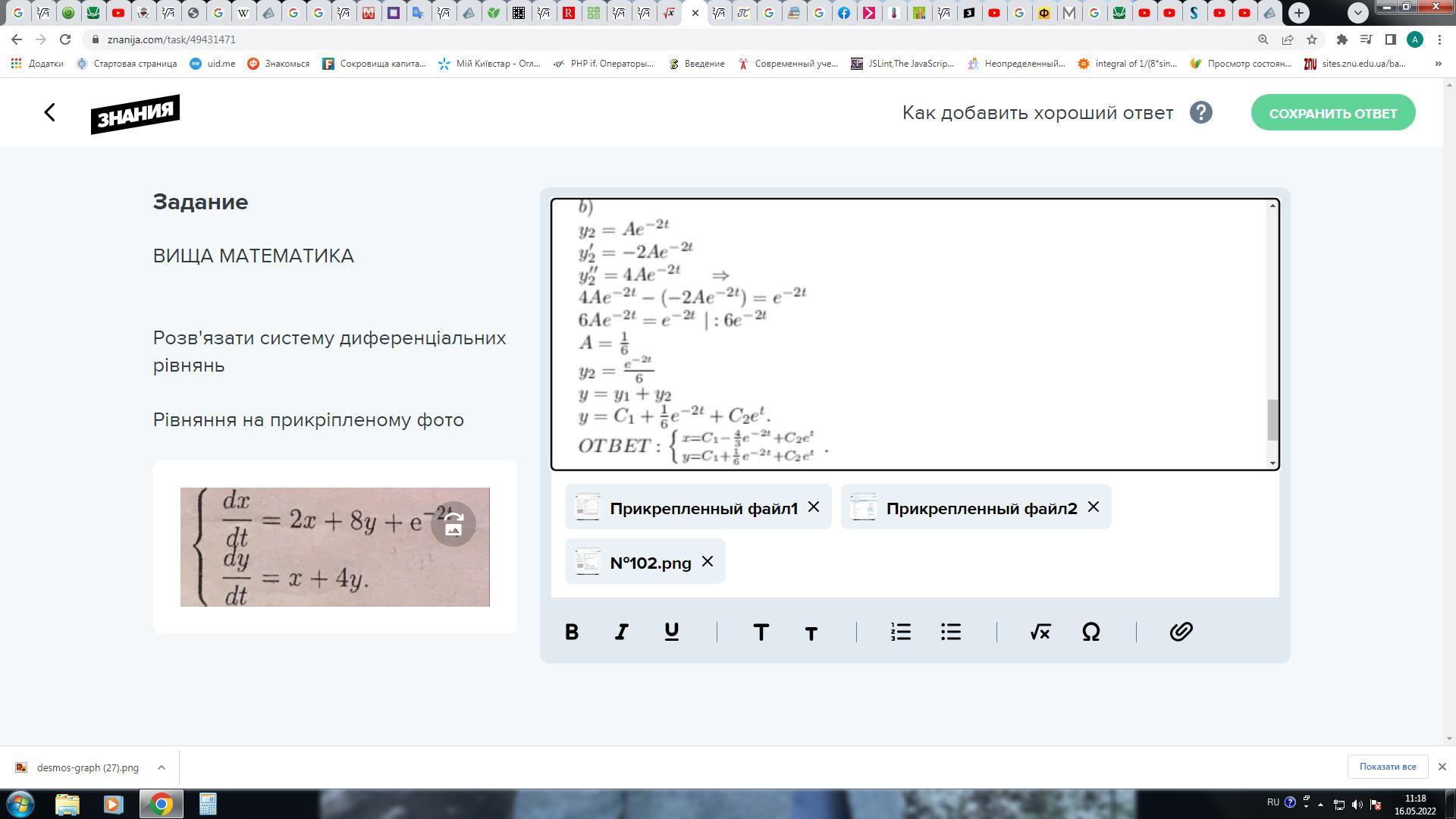
Розв'язати систему диференціальних рівнянь
Рівняння на прикріпленому фото
Приложения:
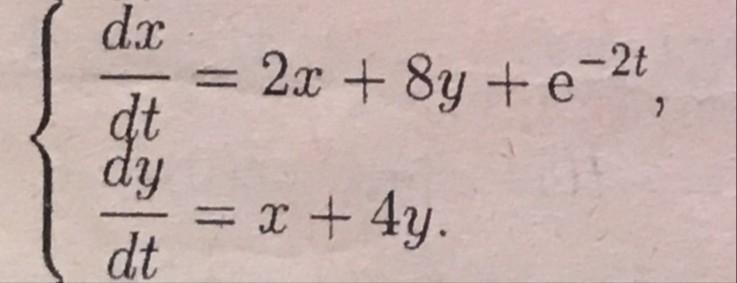
Ответы
Автор ответа:
0
Пошаговое объяснение:
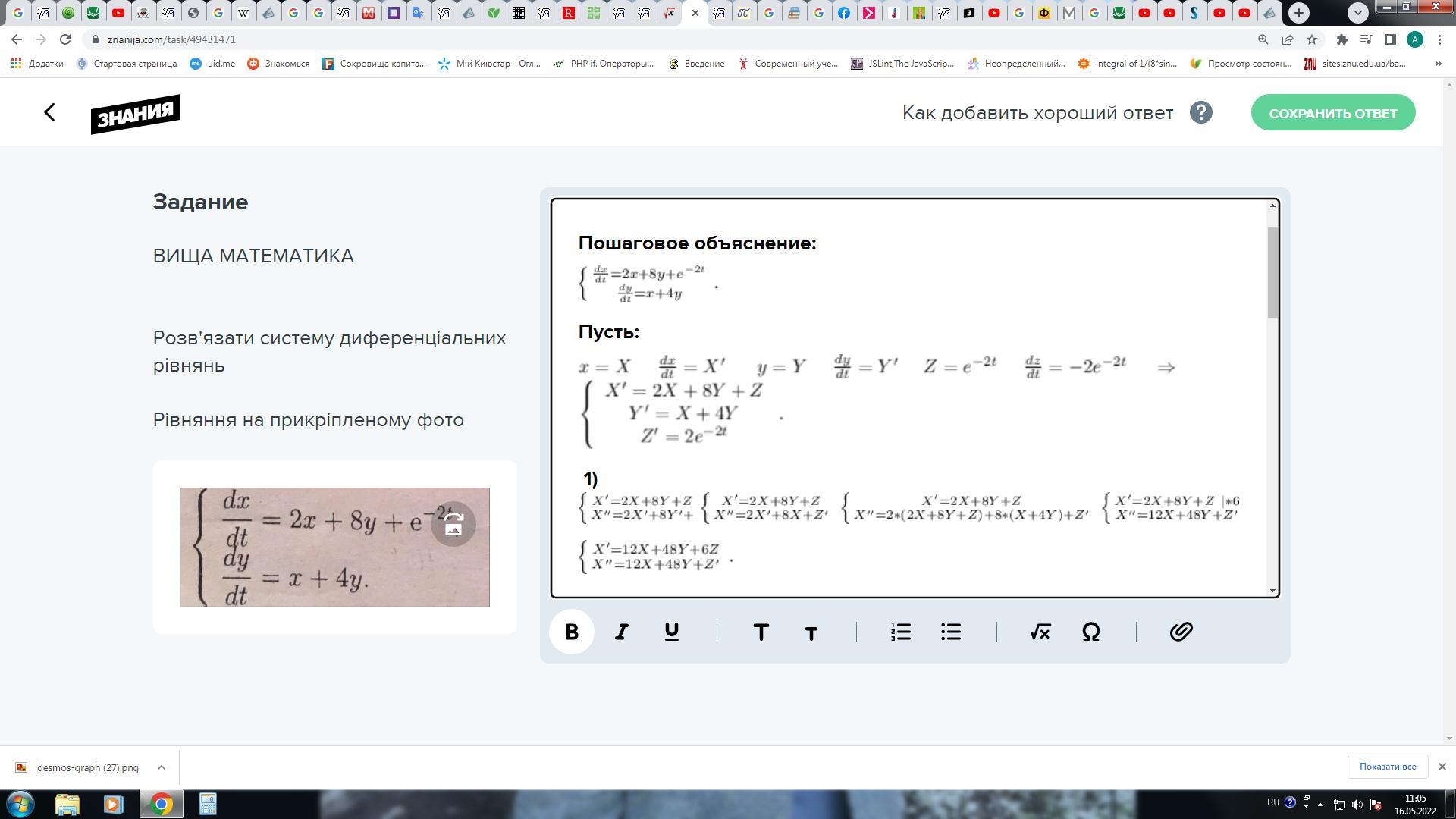
Пусть:
1)
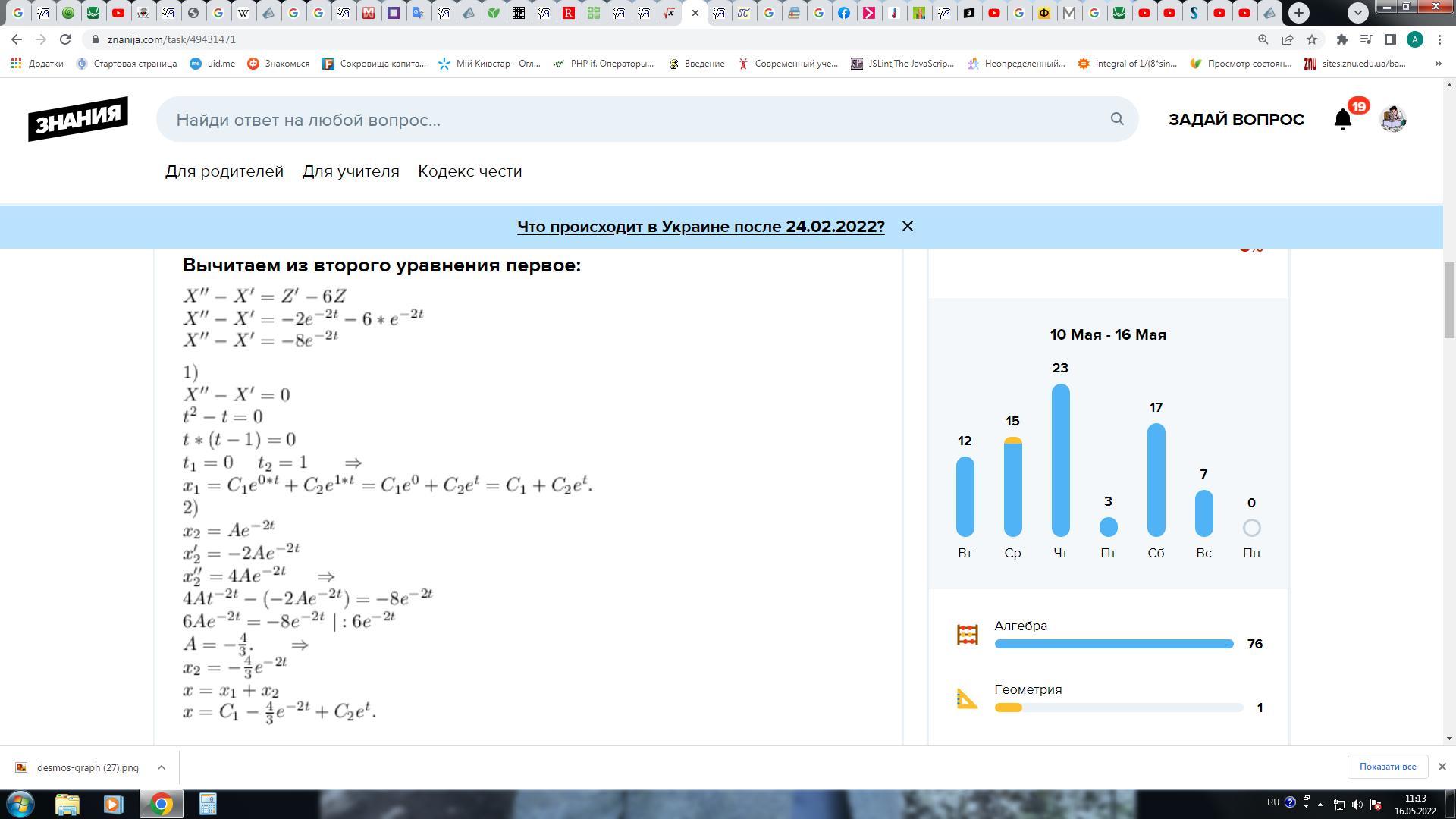
Вычитаем из второго уравнения первое:
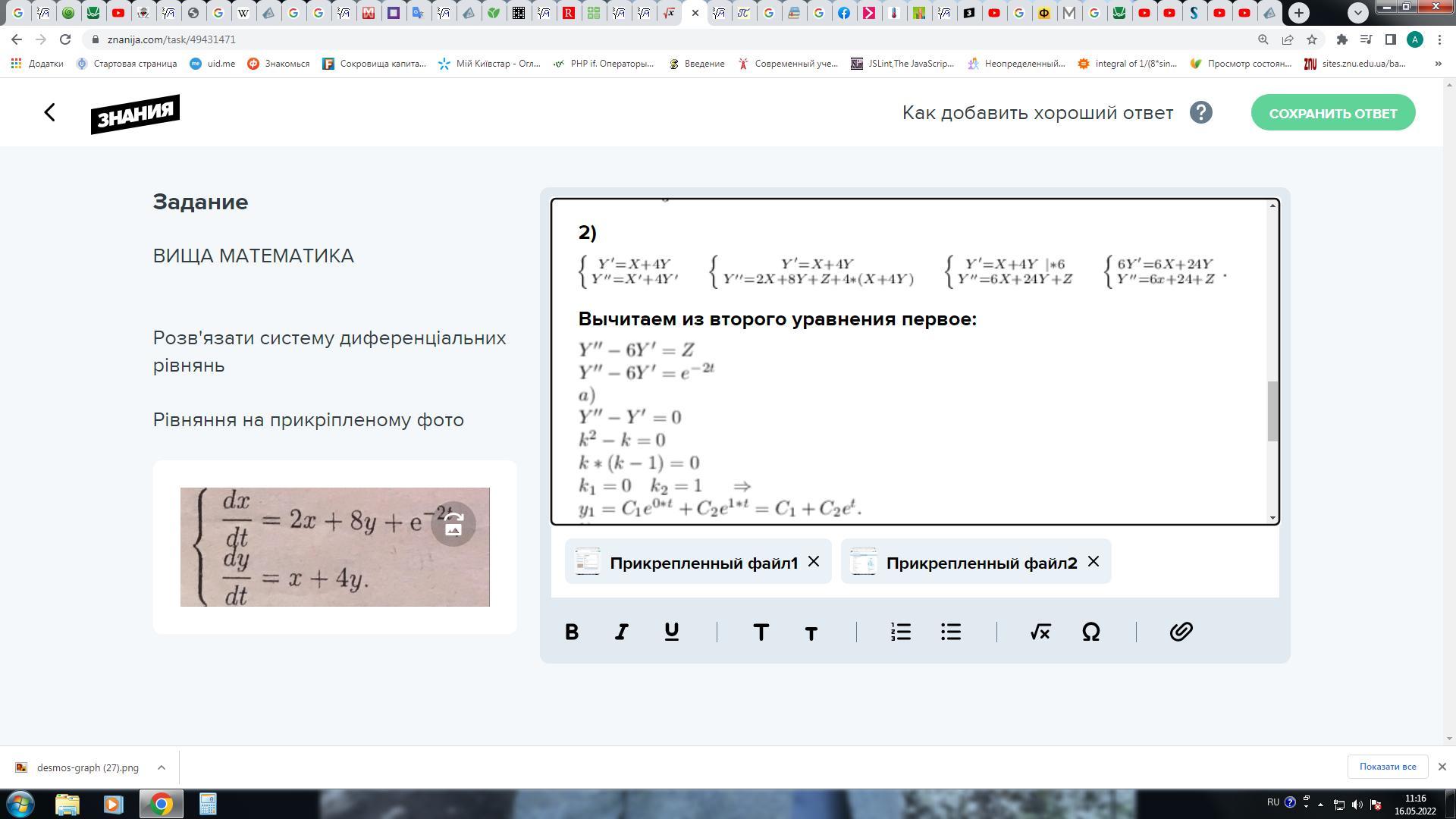
2)
Вычитаем из второго уравнения первое:
Приложения:
solka0000:
дуже дякую Вам !
1)\begin{gathered}\left \{ {{X'=2X+8Y+Z} \atop {X''=2X'+8Y'+}} \\\left \{ {{X'=2X+8Y+Z} \atop {X''=2X'+8X+Z'}} \right. \\\left \{ {{X'=2X+8Y+Z} \atop {X''=2*(2X+8Y+Z)+8*(X+4Y)+Z'}} \right\\\left \{ {{X'=2X+8Y+Z\ |*6} \atop {X''=12X+48Y+Z'} \right.\end{gathered}
тут щось важливе чи можна пропустити ?
бо мені не відкриває що там пише
Я сбросил фото.
Теперь понятно?
так ,дякую
Все зрозуміло?
так
Хай щастить
Похожие вопросы
Предмет: Русский язык,
автор: илонка0609шпионка
Предмет: Технология,
автор: София02
Предмет: Английский язык,
автор: Angelinatsymbal01
Предмет: География,
автор: ez111105
Предмет: Математика,
автор: gurinovichlena