Предмет: Геометрия,
автор: romagrigor671
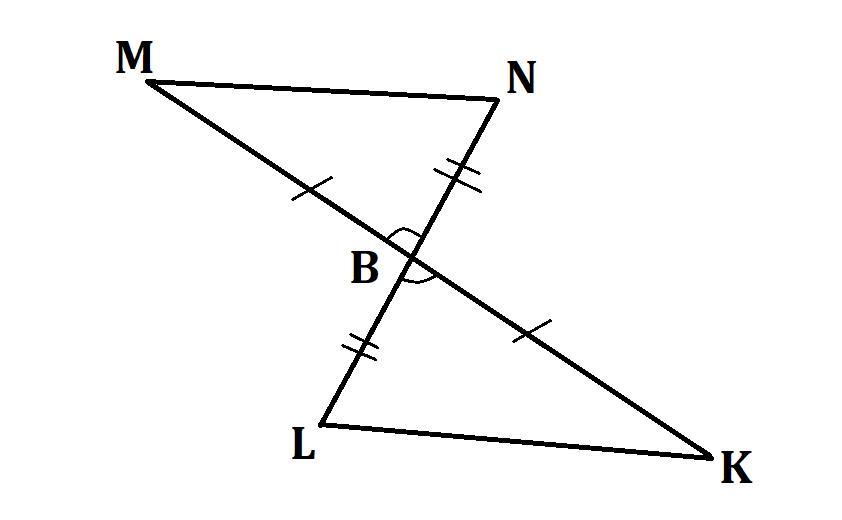
отрезки MK и NL в точке пересечения B делятся пополам. докожи что треугольник MBN = треугольник KBL
(желательно с решением:))
Ответы
Автор ответа:
0
Ответ: смотрите доказательство в объяснении.
Объяснение:
Рассмотрим ΔMBN и ΔKBL:
Так как отрезки MK и NL в точке пересечения B делятся пополам, по условию ⇒ B - середина MK и NL ⇒ MB = BK и NB = BL
- Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.
- Вертикальные углы равны.
∠MBN = ∠KBL, как вертикальные
⇒ ΔMBN = ΔKBL, по I признаку равенства треугольников (по двум сторонам и углу между ними).
ч.т.д.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kostya1641
Предмет: Русский язык,
автор: крис685
Предмет: Английский язык,
автор: Djeker
Предмет: Математика,
автор: nastikgus
Предмет: История,
автор: alesenko01