Question

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 5:2 считая от вершины угла при основании треугольника. Найдите стороны треугольника если его периметр равен 72 см​

Answer 1

Ответ:

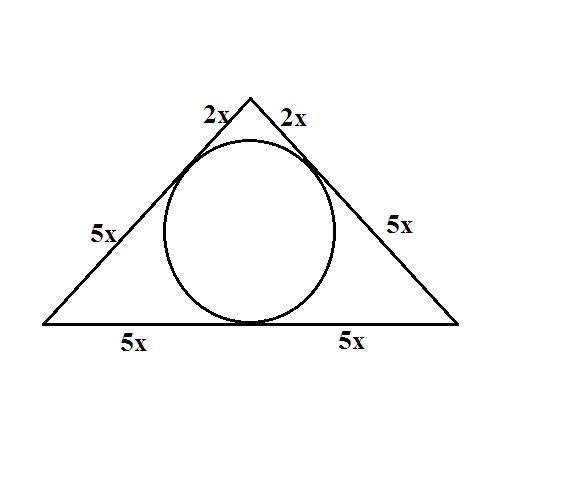
Отрезки касательных из одной точки равны. Обозначим отрезки на боковой стороне 5x и 2x. Тогда периметр равен 18x.

x=72/18 =4

a=b=7x =28

c=4x =16

Объяснение:

Answer 2

Ответ:

Объяснение:

Отрезки касательных, проведенных из одной точки равны.

Боковые стороны (5х+2х)=7х, основание (5х+5х)=10х;

периметр (7х*2+10х)=72, х=72/24=3 ⇒

боковые стороны - 7*3=21 см;

основание - 10*3=30 см.