№18 Каково количество действительных чисел удовлетворяющих следующей системе уравнений ?
A 0
B 1
C 2
D 3
E 4
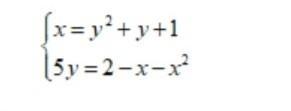
Ответы
Каково количество действительных чисел удовлетворяющих следующей системе уравнений?
{x=y²+y+1
{5y=2-x-x²
Ответ:
Существует две пары действительных чисел удовлетворяющих этой системе уравнений: (3;-2) и (1;0).
Пошаговое объяснение:
Со второго уравнения выразим х через у:
Имеем следующие системы уравнений:
В каждом из уравнений двух систем равны левые части (х=х), соответственно правые их части тоже равные. Приравниваем их и решаем два следующих уравнения:
Чтобы не решать одновременно два примера и решить всё более наглядно, начнём со второго уравнения и потом вернёмся к первому.
Проверяем, являются ли эти корни решением уравнения:
y = 0 не является корнем уравнения. Проверим корень у=(-2):
Мы пришли к тому, что второе уравнение не имеет корней. Вернёмся к первому уравнению:
Проверяем корни:
y=0 - первый корень уравнения.
y=(-2) - второй корень уравнения.