Question

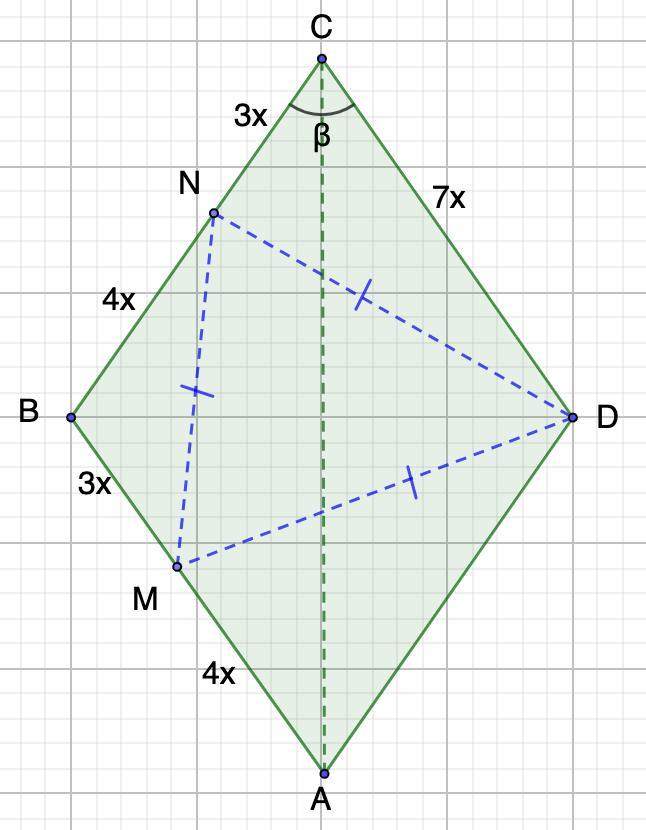
На сторонах AB и BC ромба ABCD отмечены точки M и N соответственно, причём 3⋅AM=4⋅BM, 3⋅BN=4⋅CN. Треугольник DMN оказался равносторонним. Найдите угол ACB. Ответ дайте в градусах.

Answer 1

Ответ:

Угол АСВ равен 30°.

Объяснение:

На сторонах AB и BC ромба ABCD отмечены точки M и N соответственно, причём 3⋅AM=4⋅BM, 3⋅BN=4⋅CN. Треугольник DMN оказался равносторонним. Найдите угол ACB.

Дано: ABCD - ромб;

М ∈ АВ; N ∈ BC;

3⋅AM=4⋅BM, 3⋅BN=4⋅CN;

ΔDMN - равносторонний.

Найти: ∠АСВ.

Решение:

1. 3⋅AM=4⋅BM, или

$\displaystyle \frac{AM}{BM}=\frac{4}{3}$

Пусть АМ = 4х, тогда ВМ = 3х, а АВ = 7х.

2. 3⋅BN=4⋅CN, или

$\displaystyle \frac{BN}{CN}=\frac{4}{3}$

Стороны ромба равны.

⇒ АВ = ВС = 7х

Тогда BN = 4x; CN = 3x

3. Пусть ∠С = β

Из ΔNCD выразим ND по теореме косинусов.

• Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.

ND² = NC² + CD² - 2 · NC · CD · cosβ

ND² =9x² + 49x² - 2 · 3x · 7x · cosβ = 58x² - 42x² · cosβ

4. Из ΔMBN выразим MN по теореме косинусов.

• Углы ромба, прилегающие к одной стороне, составляют в сумме 180°.

MN² = МВ² + BN² - 2 · MB · BN · cos(180° - β)

По формуле приведения cos(180° - β) = -cosβ

MN² = 9x² + 16x² + 2 · 3x · 4x · cosβ = 25x² + 24x² · cosβ

5. ND = MN (ΔDMN - равносторонний)

⇒ 58x² - 42x² · cosβ = 25x² + 24x² · cosβ

66x² · cosβ = 33x²

cosβ = 0,5

⇒ β = 60°

• В ромбе диагонали являются биссектрисами.

⇒ ∠АСВ = 60° : 2 = 30°

Угол АСВ равен 30°.

#SPJ1