Предмет: Геометрия,
автор: shakerv
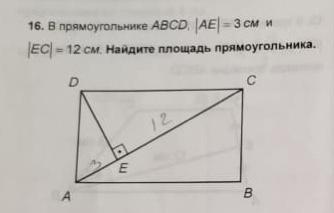
в прямоугольнике ABCD, |AE| = 3 см |AC| = 12 см найдите площадь прямоугольника.
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
DE - высота проведенная к гипотенузе - DE=√(AE*EC)=√(3*12)=6 см;
Sabcd=2*Sadc, Sadc=AC*DE/2=15*6/2=45 см²;
Sabcd=45*2=90 см².
Автор ответа:
1
Ответ:
S = 90 см^2
Объяснение:
1/2 * AC * DE = 1/2 * AD * CD
AC * DE = AD * CD
AD * CD = (3 + 12) * DE
AD * CD = 15 * DE
DE = x
AD * CD = 15 * x
AD * CD =
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: SanьkaPLAYGAMES
Предмет: Химия,
автор: vadim3112